题目内容
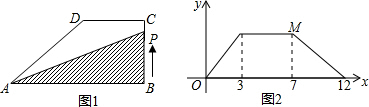
如图①,在直角梯形ABCD中,∠B=90°,DC∥AB,动点P从B点出发,由B→C→D→A沿边运动,设点P运动的路程为x,△ABP的面积为y,若关于y与x的函数图象如图②,求梯形ABCD的面积.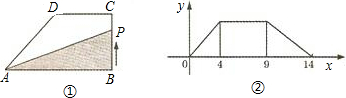
分析:作DE⊥AB,E为垂足,把直角梯形分为一个矩形和一个直角三角形,由图②知:BC=4,CD=9-4=5,DA=14-9=5,解Rt△ADE求AE,而AB=AE+BE=AE+CD,已知梯形的上底CD,下底AB,高BC可求梯形面积.
解答: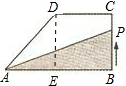 解:由图②知:BC=4
解:由图②知:BC=4
CD=9-4=5
DA=14-9=5 (6分)
作DE⊥AB,E为垂足
在Rt△ADE中,DA=5,DE=CB=4
∴AE=3
∴AB=AE+EB=AE+DC=3+5=8 (6分)
∴S梯形ABCD=
(DC+AB)•BC=
(5+8)×4=26.(2分)
 解:由图②知:BC=4
解:由图②知:BC=4CD=9-4=5
DA=14-9=5 (6分)
作DE⊥AB,E为垂足
在Rt△ADE中,DA=5,DE=CB=4
∴AE=3
∴AB=AE+EB=AE+DC=3+5=8 (6分)
∴S梯形ABCD=
| 1 |
| 2 |
| 1 |
| 2 |
点评:通过观察三角形面积变化的情况,求出梯形有关边长,同时,运用了勾股定理,围绕梯形计算面积的公式求相关量.

练习册系列答案
相关题目
 如图1,在直角梯形ABCD中,动点P从点B出发,沿BC,CD运动至点D停止.设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则△BCD的面积是( )
如图1,在直角梯形ABCD中,动点P从点B出发,沿BC,CD运动至点D停止.设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则△BCD的面积是( )| A、3 | B、4 | C、5 | D、6 |