Question

【题目】根据问题进行证明：
（1）已知：如图，在正方形ABCD中，点E在边CD上，AQ⊥BE于点Q，DP⊥AQ于点P，求证：AP=BQ．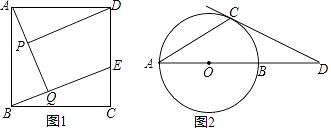
（2）如图，已知AB是⊙O的直径，AC是⊙O的弦，过点C的切线交AB的延长线于点D且∠A=∠D．求∠D的度数．

Answer 1

【答案】
（1）解：∵四边形ABCD为正方形，

∴AD=BA，∠BAD=90°，即∠BAQ+∠DAP=90°，

∵DP⊥AQ，

∴∠ADP+∠DAP=90°，

∴∠BAQ=∠ADP，

∵AQ⊥BE于点Q，DP⊥AQ于点P，

∴∠AQB=∠DPA=90°，

在△AQB和△DPA中，

∵ ，

∴△AQB≌△DPA（AAS），

∴AP=BQ；

（2）如图，连接OC，

∵CD是⊙O 的切线，

∴OC⊥CD，

∴∠OCD=90°，

∴∠COB+∠D=90°，

由圆周角定理得∠COB=2∠A，

∵∠A=∠D，

∴2∠A+∠A=90°，

∴∠A=30°，

∴∠D=30°．

【解析】（1）由正方形的性质知AD=BA、∠BAD=90°，由AQ⊥BE、DP⊥AQ知∠BAQ=∠ADP、∠AQB=∠DPA=90°，即可证△AQB≌△DPA得AP=BQ；（2）由切线的性质知∠OCD=90°即∠COB+∠D=90°，由圆周角定理知∠COB=2∠A，结合∠A=∠D可得答案．
【考点精析】解答此题的关键在于理解正方形的性质的相关知识，掌握正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形，以及对切线的性质定理的理解，了解切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径．