题目内容
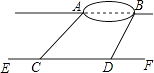
【题目】如图,四边形ABCD内接于⊙O,且BD为直径,∠ACB=45°,过A点的AC的垂线交BC的延长线于点E.

(1)求证:BE=CD;
(2)如果AD= ![]() ,求图中阴影的面积.
,求图中阴影的面积.
【答案】
(1)
解:∵BD为⊙O的直径,
∴∠BAC=90°,
∵∠ACB=45°,
∴∠ADB=∠ACB=45°,
∵AE⊥AC,
∴△ADE与△ABD是等腰直角三角形,
∴AE=AC,AB=AD,∠EAC=∠BAD=90°,
∴∠EAB=∠CAD,
在△ABE与△ADC中,  ,
,
∴△ABE≌△ADC,
∴BE=CD;
(2)
解:连接AO,则∠AOD=90°,

∵AD= ![]() ,
,
∴AO=OD=1,
∴S阴影=S扇形﹣S△AOD= ![]() ﹣
﹣ ![]() ×1×1=
×1×1= ![]() ﹣
﹣ ![]() .
.

【解析】(1)由BD为⊙O的直径,得到∠BAC=90°,根据圆周角定理得到∠ADB=∠ACB=45°,推出△ADE与△ABD是等腰直角三角形,根据全等三角形的性质即可得到结论;(2)连接AO,则∠AOD=90°,根据勾股定理得到AO=OD=1,根据图形的面积公式即可得到结论.
【考点精析】认真审题,首先需要了解圆内接四边形的性质(把圆分成n(n≥3):1、依次连结各分点所得的多边形是这个圆的内接正n边形2、经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形),还要掌握扇形面积计算公式(在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2))的相关知识才是答题的关键.

【题目】某校为了选拔学生参加“汉字听写大赛”,对九年级一班、二班各10名学生进行汉字听写测试.计分采用10分制(得分均取整数),成绩达到6分或6分以上为及格,得到9分为优秀,成绩如表1所示,并制作了成绩分析表(表2).
表1
一班 | 5 | 8 | 8 | 9 | 8 | 10 | 10 | 8 | 5 | 5 |
二班 | 10 | 6 | 6 | 9 | 10 | 4 | 5 | 7 | 10 | 8 |
表2
班级 | 平均数 | 中位数 | 众数 | 方差 | 及格率 | 优秀率 |
一班 | 7.6 | 8 | a | 3.82 | 70% | 30% |
二班 | b | 7.5 | 10 | 4.94 | 80% | 40% |
(1)在表2中,a= , b=;
(2)有人说二班的及格率、优秀率均高于一班,所以二班比一班好;但也有人认为一班成绩比二班好,请你给出坚持一班成绩好的两条理由;
(3)一班、二班获满分的中同学性别分别是1男1女、2男1女,现从这两班获满分的同学中各抽1名同学参加“汉字听写大赛”,用树状图或列表法求出恰好抽到1男1女两位同学的概率.