题目内容
 如图,已知△ABC中,AB=AC,∠A=36°.
如图,已知△ABC中,AB=AC,∠A=36°.(1)尺规作图:在AC上求作一点P,使BP+PC=AB;(保留作图痕迹,不写作法)
(2)在已作的图形中,连接PB,以点P为圆心,PB长为半径画弧交AC的延长线于点E,若BC=2cm,求扇形PBE的面积.
分析:(1)由于△ABC中,AB=AC,∠A=36°,由此可以得到∠ABC=∠ACB=72°,所以作∠ABC的平分线BP之后可以得到△ABP,△BPC它们都是等腰三角形,由此即可得到满足BP+PC=AB的P的点;
(2)根据(1)的结论知道BC=BP=AB,并且∠BPC=72°,然后利用扇形的面积公式即可求出扇形PBE的面积.
(2)根据(1)的结论知道BC=BP=AB,并且∠BPC=72°,然后利用扇形的面积公式即可求出扇形PBE的面积.
解答: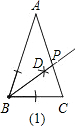 解:(1)如图射线BD交AC于P,P即为所求;
解:(1)如图射线BD交AC于P,P即为所求;
(2)如图,根据作图得BP平分∠ABP=∠CBP,
而在△ABC中,AB=AC,∠A=36°,
∴∠ABC=∠ACB=72°,
∴△PAB是等腰三角形,△BCP是等腰三角形,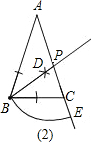
∴AP=BP=BC=PE=2,∠BPC=72°,
∴S扇形PBE=
=
π.
 解:(1)如图射线BD交AC于P,P即为所求;
解:(1)如图射线BD交AC于P,P即为所求;(2)如图,根据作图得BP平分∠ABP=∠CBP,
而在△ABC中,AB=AC,∠A=36°,
∴∠ABC=∠ACB=72°,
∴△PAB是等腰三角形,△BCP是等腰三角形,

∴AP=BP=BC=PE=2,∠BPC=72°,
∴S扇形PBE=
| 72×π×22 |
| 360 |
| 4 |
| 5 |
点评:此题主要考查了等腰三角形的特殊性质,特殊也考查了扇形面积的计算.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
 如图,已知△ABC中,AB=AC,E、F分别在AB、AC上且AE=CF.
如图,已知△ABC中,AB=AC,E、F分别在AB、AC上且AE=CF. 如图,已知△ABC中,P是AB上一点,连接CP,以下条件不能判定△ACP∽△ABC的是( )
如图,已知△ABC中,P是AB上一点,连接CP,以下条件不能判定△ACP∽△ABC的是( ) (2012•梓潼县一模)如图,已知△ABC中,∠C=90°,AC=4,BC=3,则sinA=( )
(2012•梓潼县一模)如图,已知△ABC中,∠C=90°,AC=4,BC=3,则sinA=( ) 如图,已知△ABC中,BC=8,BC边上的高h=4,D为BC上一点,EF∥BC交AB于E,交AC于F(EF不过A、B),设E到BC的距离为x,△DEF的面积为y,那么y关于x的函数图象大致是( )
如图,已知△ABC中,BC=8,BC边上的高h=4,D为BC上一点,EF∥BC交AB于E,交AC于F(EF不过A、B),设E到BC的距离为x,△DEF的面积为y,那么y关于x的函数图象大致是( ) 如图,已知△ABC中,AB=AC,D是BC中点,则下列结论不正确的是( )
如图,已知△ABC中,AB=AC,D是BC中点,则下列结论不正确的是( )