题目内容
【题目】如图,在直角坐标系中,点A的坐标为(-2,0),OB=OA,且∠AOB=120°.
(1)求经过A、O、B三点的抛物线的解析式;
(2)在(1)中抛物线的对称轴上是否存在点C,使△OBC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由;
(3)若点M为抛物线上一点,点N为对称轴上一点,是否存在点M、N使得A、O、M、N构成的四边形是平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)(-1,
;(2)(-1,![]() );(3) M1(-1,-
);(3) M1(-1,-![]() ),M2(-3,
),M2(-3,![]() ),M3(1,
),M3(1,![]() ).
).
【解析】
(1)先确定出点B坐标,再用待定系数法即可;
(2)先判断出使△BOC的周长最小的点C的位置,再求解即可;
(3)分OA为对角线、为边这两种情况进行讨论计算即可得出答案.
(1)如图所示,过点B作BD⊥x轴于点D,
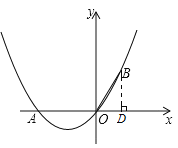
∵点A的坐标为(-2,0),OB=OA,
∴OB=OA=2,
∵∠AOB=120°,
∴∠BOD=60°,
在Rt△OBD中,∠ODB=90°,
∴∠OBD=30°,
∴OD=1,DB=![]() ,
,
∴点B的坐标是(1, ![]() ),
),
设所求抛物线的解析式为y=ax2+bx+c,
由已知可得:
 ,
,
解得: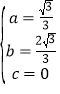
∴所求抛物线解析式为![]() ;
;
(2)存在.
如图所示,
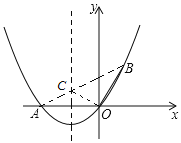
∵△BOC的周长=OB+BC+CO,
又∵OB=2,
∴要使△BOC的周长最小,必须BC+CO最小,
∵点O和点A关于对称轴对称,
∴连接AB与对称轴的交点即为点C,
由对称可知,OC=OA,
此时△BOC的周长=OB+BC+CO=OB+BC+AC;
点C为直线AB与抛物线对称轴的交点,
设直线AB的解析式为y=kx+b,
将点A(2,0),B(1,![]() )分别代入,得:
)分别代入,得:
![]() ,
,
解得: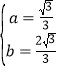 ,
,
∴直线AB的解析式为y=![]() x+
x+![]() ,
,
当x=1时span>,y=![]() ,
,
∴所求点C的坐标为(1,![]() );
);
(3)如图所示,
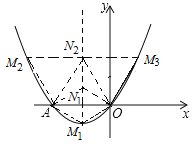
①当以OA为对角线时,
∵OA与MN互相垂直且平分,
∴点M1(1,![]() ),
),
②当以OA为边时,
∵OA=MN且OA∥MN,
即MN=2,MN∥x轴,
设N(1,t),
则M(3,t)或(1,t)
将M点坐标代入![]() ,
,
解得,t=![]() ,
,
∴M2(3,![]() ),M3 (1,
),M3 (1,![]() )
)
综上:点M的坐标为:(-1,-![]() ),或(-3,
),或(-3,![]() )或(1,
)或(1,![]() ).
).

 53随堂测系列答案
53随堂测系列答案