题目内容
【题目】已知:如图,在梯形ABCD中,AD∥BC,BC=DC,CF平分∠BCD,DF∥AB,BF的延长线交DC于点E.求证: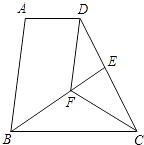
(1)△BFC≌△DFC;
(2)AD=DE.
【答案】
(1)证明:∵CF平分∠BCD,
∴∠BCF=∠DCF.
在△BFC和△DFC中,

∴△BFC≌△DFC(SAS)
(2)证明:连接BD. 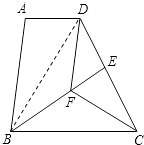
∵△BFC≌△DFC,
∴BF=DF,∴∠FBD=∠FDB.
∵DF∥AB,
∴∠ABD=∠FDB.
∴∠ABD=∠FBD.
∵AD∥BC,
∴∠BDA=∠DBC.
∵BC=DC,
∴∠DBC=∠BDC.
∴∠BDA=∠BDC.
又∵BD是公共边,
∴△BAD≌△BED(ASA).
∴AD=DE.
【解析】(1)根据题意和SAS得得得△BFC≌△DFC;(2)由(1)知△BFC≌△DFC,根据对应边相等,得到BF=DF,再根据等腰三角形的性质得到∠FBD=∠FDB,由已知DF∥AB,再由ASA得到△BAD≌△BED,根据全等三角形的对应边相等,得到AD=DE.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目