题目内容
已知α,β是△ABC的两个角,且sinα,tanβ是方程2x2-3x+1=0的两根,则△ABC是
- A.锐角三角形
- B.直角三角形或钝角三角形
- C.钝角三角形
- D.等边三角形
B
分析:先解出方程的两根,讨论sinα,tanβ的值.∵在三角形中,角的范围是(0,180°),∴sinα必大于0,此时只要考虑tanβ的值即可,若tanβ>0,则β为锐角;tanβ小于0,则β为钝角.再把x的两个值分别代入sinα,tanβ中,可求出α,β的值,从而判断△ABC的形状.
解答:由2x2-3x+1=0得:(2x-1)(x-1)=0,∴x= 或x=1.
或x=1.
∴sinα>0,tanβ>0
若sinα= ,tanβ=1,则α=30°,β=45°,γ=180°-30°-45°=105°,
,tanβ=1,则α=30°,β=45°,γ=180°-30°-45°=105°,
∴△ABC为钝角三角形.
若sinα=1,tanβ= ,则α=90°,β<90°,△ABC为直角三角形.
,则α=90°,β<90°,△ABC为直角三角形.
故选B.
点评:本题易在α,β上的取值出错,学生常常解出方程的两根后不知道如何判断,因此在解答时我们可对x的值分类讨论,从而判断出△ABC的形状.
分析:先解出方程的两根,讨论sinα,tanβ的值.∵在三角形中,角的范围是(0,180°),∴sinα必大于0,此时只要考虑tanβ的值即可,若tanβ>0,则β为锐角;tanβ小于0,则β为钝角.再把x的两个值分别代入sinα,tanβ中,可求出α,β的值,从而判断△ABC的形状.
解答:由2x2-3x+1=0得:(2x-1)(x-1)=0,∴x=
 或x=1.
或x=1.∴sinα>0,tanβ>0
若sinα=
 ,tanβ=1,则α=30°,β=45°,γ=180°-30°-45°=105°,
,tanβ=1,则α=30°,β=45°,γ=180°-30°-45°=105°,∴△ABC为钝角三角形.
若sinα=1,tanβ=
 ,则α=90°,β<90°,△ABC为直角三角形.
,则α=90°,β<90°,△ABC为直角三角形.故选B.
点评:本题易在α,β上的取值出错,学生常常解出方程的两根后不知道如何判断,因此在解答时我们可对x的值分类讨论,从而判断出△ABC的形状.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
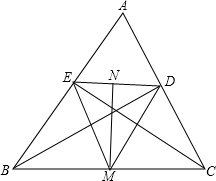 已知BD,CE是△ABC的两条高,M、N分别为BC、DE的中点,勇敢猜一猜:
已知BD,CE是△ABC的两条高,M、N分别为BC、DE的中点,勇敢猜一猜: