题目内容
(本题满分14分)如图,二次函数![]() 与x轴交于A、B两点,与y轴交于C点,点P从A
与x轴交于A、B两点,与y轴交于C点,点P从A
 点出发,以1个单位每秒的速度向点B运动,点Q同时从C点出发,以相同的速度向y轴正方向运动,运动时间为t秒,点P到达B点时,点Q同时停止运动。设PQ交直线AC于点G。
点出发,以1个单位每秒的速度向点B运动,点Q同时从C点出发,以相同的速度向y轴正方向运动,运动时间为t秒,点P到达B点时,点Q同时停止运动。设PQ交直线AC于点G。
(1)求直线AC的解析式;
(2)设△PQC的面积为S,求S关于t的函数解析式;
(3)在y轴上找一点M,使△MAC和△MBC都是等
腰三角形。直接写出所有满足条件的M点的坐标;
(4)过点P作PE⊥AC,垂足为E,当P点运动时,
线段EG的长度是否发生改变,请说明理由。
解:(1)![]() 2分
2分
(2) 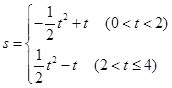 4分
4分
(3)一共四个点,(0,![]() ),(0,0),(0,
),(0,0),(0,![]() ),(0,-2)。4分
),(0,-2)。4分
(4)当P点运动时,线段EG的长度不发生改变,为定值![]() 。
。
当0<t<2时,过G作GH⊥y轴,垂足为H.
由AP=t,可得AE= ![]() .
.
由相似可得GH=![]() ,
,
所以GC=![]()
![]() .
.
于是,GE=AC-AE-GC=![]() .
.
即GE的长度不变.
当2<t ≤ 4时,同理可证.
综合得:当P点运动时,线段EG的长度不发生改变,为定值![]() 4分
4分
解析:求函数解析式一般做法是把函数图象上点的坐标代入;另外此题还是几何与代数的结合

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目



 与x轴交于A、B两点,与y轴交于C点,点P从A
与x轴交于A、B两点,与y轴交于C点,点P从A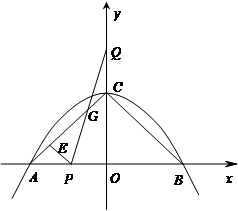 点出发,以1个单位每秒的速度向点B运动,点Q同时从C点出发,以相同的速度向y轴正方向运动,运动时间为t秒,点P到达B点时,点Q同时停止运动。设PQ交直线AC于点G。
点出发,以1个单位每秒的速度向点B运动,点Q同时从C点出发,以相同的速度向y轴正方向运动,运动时间为t秒,点P到达B点时,点Q同时停止运动。设PQ交直线AC于点G。 与x轴交于A、B两点,与y轴交于C点,点P从A
与x轴交于A、B两点,与y轴交于C点,点P从A 点出发,以1个单位每秒的速度向点B运动,点Q同时从C点出发,以相同的速度向y轴正方向运动,运动时间为t秒,点P到达B点时,点Q同时停止运动。设PQ交直线AC于点G。
点出发,以1个单位每秒的速度向点B运动,点Q同时从C点出发,以相同的速度向y轴正方向运动,运动时间为t秒,点P到达B点时,点Q同时停止运动。设PQ交直线AC于点G。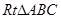 中,
中,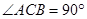 ,
, 是斜边
是斜边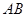 上的中线,
上的中线,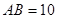 ,
,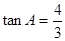 ,点
,点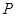 是
是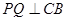 ,交
,交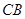 延长线于点
延长线于点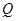 ,
, .
.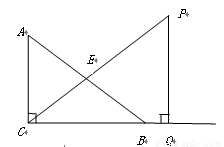
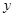 关于
关于 的函数关系式及定义域;(4分)
的函数关系式及定义域;(4分)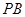 ,当
,当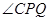 时,求
时,求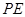 的长;(4分)
的长;(4分)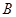 作
作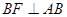 交
交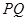 于
于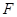 ,当
,当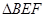 和
和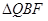 相似时,求
相似时,求