题目内容
(本题满分14分)如图①,将边长为4cm的正方形纸片ABCD沿EF折叠(点E、F分别在边AB、CD上),使点B落在AD边上的点 M处,点C落在点N处,MN与CD交于点P, 连接EP.
⑴如图②,若M为AD边的中点,①△AEM的周长=____ _cm;②求证:EP=AE+DP;

⑵随着落点M在AD边上取遍所有的位置(点M不与A、D重合),△PDM的周长是否发生变化?请说明理由.

⑴①6………………………………………………………………………………2分
②证明:取EP中点G,连接MG,在梯形AEPD中
∵M、G分别为AD、EP的中点
∴![]() ……………………………………………………4分
……………………………………………………4分
由折叠,得∠EMP=∠B=90°
又G为EP的中点
∴MG=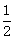 EP………………………………………………………………6分
EP………………………………………………………………6分
∴EP=AE+DP ……………………………………………………………7分
⑵△PDM的周长保持不变 ……………………………………………………8分
证明:设AM=xcm,则DM=(4-x)cm …………………………………9分
Rt△EAM中,由![]()
![]() …………………………………………………10分
…………………………………………………10分
∵∠AME+∠AEM=90°
∠AME+∠PMD=90°
∴∠AEM=∠PMD……………………………………………………11分
又∵∠A=∠D=90°
∴△PDM∽△MAE……………………………………………………12分
∴![]() ………………………………………………………13分
………………………………………………………13分
即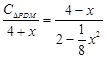
∴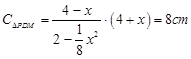 ……………………………………14分
……………………………………14分
∴△PDM的周长保持不变.
解析:略

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目

 与x轴交于A、B两点,与y轴交于C点,点P从A
与x轴交于A、B两点,与y轴交于C点,点P从A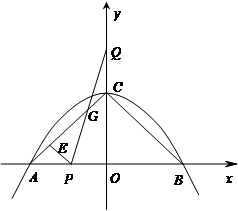 点出发,以1个单位每秒的速度向点B运动,点Q同时从C点出发,以相同的速度向y轴正方向运动,运动时间为t秒,点P到达B点时,点Q同时停止运动。设PQ交直线AC于点G。
点出发,以1个单位每秒的速度向点B运动,点Q同时从C点出发,以相同的速度向y轴正方向运动,运动时间为t秒,点P到达B点时,点Q同时停止运动。设PQ交直线AC于点G。 与x轴交于A、B两点,与y轴交于C点,点P从A
与x轴交于A、B两点,与y轴交于C点,点P从A 点出发,以1个单位每秒的速度向点B运动,点Q同时从C点出发,以相同的速度向y轴正方向运动,运动时间为t秒,点P到达B点时,点Q同时停止运动。设PQ交直线AC于点G。
点出发,以1个单位每秒的速度向点B运动,点Q同时从C点出发,以相同的速度向y轴正方向运动,运动时间为t秒,点P到达B点时,点Q同时停止运动。设PQ交直线AC于点G。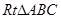 中,
中,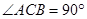 ,
, 是斜边
是斜边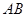 上的中线,
上的中线,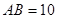 ,
,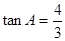 ,点
,点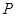 是
是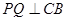 ,交
,交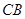 延长线于点
延长线于点 ,
, .
.
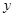 关于
关于 的函数关系式及定义域;(4分)
的函数关系式及定义域;(4分)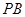 ,当
,当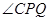 时,求
时,求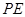 的长;(4分)
的长;(4分)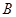 作
作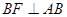 交
交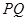 于
于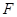 ,当
,当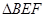 和
和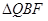 相似时,求
相似时,求