题目内容
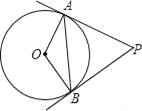
【题目】如图,D为AB上一点,△ACE≌△BCD,AD2+DB2=DE2 , 试判断△ABC的形状,并说明理由. 
【答案】解:△ABC是等腰直角三角形,
理由是:∵△ACE≌△BCD,
∴AC=BC,∠EAC=∠B,AE=BD,
∵AD2+DB2=DE2,
∴AD2+AE2=DE2,
∴∠EAD=90°,
∴∠EAC+∠DAC=90°,
∴∠DAC+∠B=90°,
∴∠ACB=180°﹣90°=90°,
∵AC=BC,
∴△ABC是等腰直角三角形.
【解析】根据全等三角形的性质得出AC=BC,∠EAC=∠B,AE=BD,根据勾股定理的逆定理得出∠EAD=90°,求出∠ACB=90°,即可求出答案.
【考点精析】本题主要考查了全等三角形的性质和勾股定理的逆定理的相关知识点,需要掌握全等三角形的对应边相等; 全等三角形的对应角相等;如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形才能正确解答此题.

练习册系列答案
相关题目
【题目】下表是七年级三班30名学生期末考试数学成绩表(已破损)
成绩(分) | 50 | 60 | 70 | 80 | 90 | 100 |
人数(人) | 2 | 5 | 7 | 3 |
已知该班学生期末考试数学成绩平均分是76分.
(1)求该班80分和90分的人数分别是多少?
(2)设该班30名学生成绩的众数为a,中位数为b,求a+b的值.