题目内容
已知线段AB=12cm,直线AB上有一点C,且BC=6cm,M是线段AC的中点,求线段AM的长.
分析:根据题意画出符合条件的两种情况,求出AC的长,根据AM=
AC求出即可.
| 1 |
| 2 |
解答:解:(1)当点C在线段AB上时,如图1,
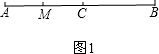
∵AB=12cm,BC=6cm,
∴AC=AB-BC=6cm,
∵M是AC的中点,
∴AM=
AC,
∴AM=
×6cm=3cm;
(2)当点C在线段AB的延长线上时,如图2,

∵AB=12cm,BC=6cm,
∴AC=AB+BC=18cm,
∵M是AC的中点,
∴AM=
AC,
∴AM=
×18cm=9cm,
∴线段AM的长为3cm或9cm.

∵AB=12cm,BC=6cm,
∴AC=AB-BC=6cm,
∵M是AC的中点,
∴AM=
| 1 |
| 2 |
∴AM=
| 1 |
| 2 |
(2)当点C在线段AB的延长线上时,如图2,

∵AB=12cm,BC=6cm,
∴AC=AB+BC=18cm,
∵M是AC的中点,
∴AM=
| 1 |
| 2 |
∴AM=
| 1 |
| 2 |
∴线段AM的长为3cm或9cm.
点评:本题考查了两点间的距离的应用,注意:在求解没有图形的几何题时,应根据题意画图,同时注意图形的多样性,以免漏解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如图,已知线段AB=20cm,C为直线AB上一点,且AC=4cm,M,N分别是AC、BC的中点,则MN等于( )cm.


| A、13 | B、12 | C、10或8 | D、10 |
已知线段AB=1,C是AB的黄金分割点,AC>BC,则BC的长为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,已知线段AB、BC的中垂线l1,l2交于点M,则线段AM与线段CM的比值是( )
如图,已知线段AB、BC的中垂线l1,l2交于点M,则线段AM与线段CM的比值是( )