题目内容
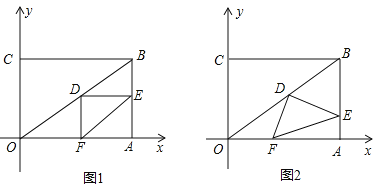
【题目】平面直角坐标系xOy中，点P（a，b）经过某种变换后得到的对应点为
. 已知A，B，C是不共线的三个点，它们经过这种变换后，得到的对应点分别为
. 若△ABC的面积为
，△
的面积为
，则用等式表示与的关系为
A. 
B. 
C. 
D. 
【答案】D
【解析】
由点P（a，b）经过变换后得到的对应点为
可知，点P的横纵坐标先缩小
，再向右向下平移；由此可知线段AB，BC，AC的长度变再变换后为原来的，则可以得出答案.
由点P（a，b）经过变换后得到的对应点为可知，点P的横纵坐标先缩小，再向右向下平移.因为点A，B，C变换得到
，根据平移的性质，向右向下平移不改变点A，B，C三点的距离，但是横纵坐标先缩小，会使得线段AB，BC，AC的长度变再变换后为原来的，则根据面积公式可知，变换后的面积为原来的
.
故答案选择D项.
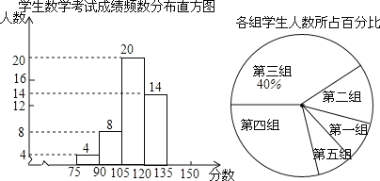
名校练考卷期末冲刺卷系列答案
【题目】某医药研究所开发一种新的药物，据监测，如果成年人按规定的剂量服用，服药后2小时，每毫升血液中的含药量达到最大值，之后每毫升血液中的含药量逐渐衰减．若一次服药后每毫升血液中的含药量y（单位：微克）与服药后的时间t（单位：小时）之间近似满足某种函数关系，下表是y与t的几组对应值，其部分图象如图所示．
t | 0 | 1 | 2 | 3 | 4 | 6 | 8 | 10 | … |
y | 0 | 2 | 4 | 2.83 | 2 | 1 | 0.5 | 0.25 | … |
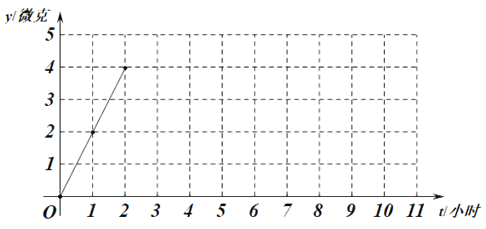
（1）在所给平面直角坐标系中，继续描出上表中已列出数值所对应的点（t，y），并补全该函数的图象；
（2）结合函数图象，解决下列问题：
①某病人第一次服药后5小时，每毫升血液中的含药量约为_______微克；若每毫升血液中含药量不少于0.5微克时治疗疾病有效，则第一次服药后治疗该疾病有效的时间共持续约_______小时；
②若某病人第一次服药后8小时进行第二次服药，第二次服药对血液中含药量的影响与第一次服药相同，则第二次服药后2小时，每毫升血液中的含药量约为_______微克．
