题目内容
【题目】如图，抛物线y＝ax2+bx+c(a≠0)的对称轴为直线x＝1，与x轴的一个交点坐标为(﹣1，0)，其部分图象如图所示，下列结论中正确的有( )
①4ac＜b2
②方程ax2+bx+c＝0的两个根是x1＝﹣1，x2＝3
③3a+c＞0
④当y＞0时，取值范围是﹣1≤x≤3
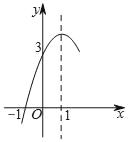
A. ①②B. ①②③C. ①③④D. ②④
【答案】A
【解析】
利用抛物线与x轴的交点个数可对①进行判断；利用抛物线的对称性得到抛物线与x轴的一个交点坐标为（3，0），则可对②进行判断；由对称轴方程得到b＝2a，然后根据x＝1时函数值为0可得到3a＋c＝0，则可对③进行判断；根据抛物线在x轴上方所对应的自变量的范围可对④进行判断．
∵抛物线与x轴有2个交点，
∴b2﹣4ac＞0，即4ac＜b2，所以①正确；
∵抛物线的对称轴为直线x＝1，
而点(﹣1，0)关于直线x＝1的对称点的坐标为(3，0)，
∴方程ax2+bx+c＝0的两个根是x1＝﹣1，x2＝3，所以②正确；
∵x＝
＝1，即b＝﹣2a，
而x＝﹣1时，y＝0，即a﹣b+c＝0，
∴a+2a+c＝0，
∴3a+c＝0，即a＝
，所以③错误；
∵抛物线与x轴的两点坐标为(﹣1，0)，(3，0)，
∴当﹣1＜x＜3时，y＞0，所以④错误．
故选：A．
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
【题目】我国农村劳动力人数有4.8亿．从目前来看，我国农民的科技水平还不高，在农村4.8亿的劳动力中，小学文化程度以下的占40%，具有初中文化程度的占48%，具有高中文化程度的占12%，受过职业技术培训的占5%，但据专家统计，他们中八成以上会进行分数、平均数、增长率等基本数学运算，能基本适应当代经济生活，这是初等数学教育的一大成就．
请根据上面的数据信息解答下列问题：
文化程度 | 人数(亿) | 会基本数学运算人数(亿) | 百分比 |
小学以下 | 1.4976 | ||
初中文化 | 2.0736 | 90% | |
高中文化 | 95% | ||
受过职业技术培训 | 0.2328 | 97% |
(1)填写下列农民受教育情况及掌握基本数学运算情况统计
(2)根据图表，求出农村劳动力中会进行基本数学运算的总人数占农村劳动力总人数的百分比；
(3)政府计划两年后使农村劳动力初、高中文化程度达到80%，那么平均每年增长的百分率是多少(精确到0.1%)？
