题目内容
【题目】如图,∠A=15°,AB=BC=CD=DE=EF,则∠DEF等于( )
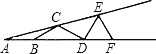
A.90° B.75° C.70° D.60°
【答案】D
【解析】
试题分析:根据已知条件,利用等腰三角形的性质及三角形的内角和外角之间的关系进行计算.
解:∵AB=BC=CD=DE=EF,∠A=15°,
∴∠BCA=∠A=15°,
∴∠CBD=∠BDC=∠BCA+∠A=15°+15°=30°,
∴∠BCD=180°﹣(∠CBD+∠BDC)=180°﹣60°=120°,
∴∠ECD=∠CED=180°﹣∠BCD﹣∠BCA=180°﹣120°﹣15°=45°,
∴∠CDE=180°﹣(∠ECD+∠CED)=180°﹣90°=90°,
∴∠EDF=∠EFD=180°﹣∠CDE﹣∠BDC=180°﹣90°﹣30°=60°,
∴∠DEF=180°﹣(∠EDF+∠EFC)=180°﹣120°=60°.
故选D.

练习册系列答案
相关题目
【题目】2016年2月上旬福州地区空气质量指数(AQI)如下表所示,空气质量指数不大于100表示空气质量优良,如果小王该月上旬来福州度假三天那么他在福州度假期间空气质量都是优良的概率是 .
2016年2月上旬福州地区空气质量指数(AQI)
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
ug/m3 | 26 | 34 | 43 | 41 | 34 | 48 | 78 | 1 15 | 59 | 45 |