题目内容
【题目】如图，已知△ABC是等边三角形，E，D，G分别在AB，BC，AC边上，且AE＝BD＝CG.连接AD，BG，CE，相交于F，M，N.
(1)求证：AD＝CE；
(2)求∠DFC的度数；
(3)试判断△FMN的形状，并说明理由．
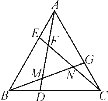
【答案】(1)见解析；(2)60°；(3)等边三角形，理由见解析.
【解析】试题分析：（1）求证ABDCAE即可证明AD＝CE；（2）由三角形外角的性质可以得到∠DFC＝∠FAC＋∠ACE＝∠FAC＋∠BAD＝60°；（3）与（2）同样的道理可证∠FMN=∠FNM=∠DFC=60°,即可证得△FMN是等边三角形。
解：(1)证明：∵△ABC是等边三角形，
∴∠BAC＝∠ABC＝60°，AB＝AC.
又∵AE＝BD，
∴△AEC≌△BDA(SAS)．
∴AD＝CE.
(2)由(1)知△AEC≌△BDA，
∴∠ACE＝∠BAD.
∴∠DFC＝∠FAC＋∠ACE＝∠FAC＋∠BAD＝60°.
(3)△FMN为等边三角形，由(2)知∠DFC＝60°，
同理可求得∠AMG＝60°，∠BNF＝60°.
∴△FMN是等边三角形．
练习册系列答案
相关题目
