题目内容
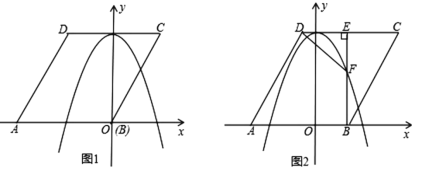
【题目】如图1,已知菱形ABCD的边长为2![]() ,点A在x轴负半轴上,点B在坐标原点。点D的坐标为(
,点A在x轴负半轴上,点B在坐标原点。点D的坐标为(![]() ,3),抛物线y=ax2+b(a≠0)经过AB、CD两边的中点.
,3),抛物线y=ax2+b(a≠0)经过AB、CD两边的中点.
(1)求这条抛物线的函数解析式;
(2)将菱形ABCD以每秒1个单位长度的速度沿x轴正方向匀速平移(如图2),过点B作BE⊥CD于点E,交抛物线于点F,连接DF.设菱形ABCD平移的时间为t秒(0<t<3)
①是否存在这样的t,使DF=![]() FB?若存在,求出t的值;若不存在,请说明理由;
FB?若存在,求出t的值;若不存在,请说明理由;
②连接FC,以点F为旋转中心,将△FEC按顺时针方向旋转180°,得△FE′C′,当△FE′C′落在x轴与抛物线在x轴上方的部分围成的图形中(包括边界)时,求t的取值范围.(直接写出答案即可)
【答案】(1)y=x2+3;(2)①t=![]() 或t=
或t=![]() ;②
;②![]()
![]() t
t![]()
【解析】
(1)根据已知条件求出AB和CD的中点坐标,然后利用待定系数法求该二次函数的解析式;
(2)①由D(![]() ,3),则平移后坐标为D(
,3),则平移后坐标为D(![]() +t,3),F(t,-t2+3);则有DF2=(
+t,3),F(t,-t2+3);则有DF2=(![]() +t-t)2+(-t2+3-3)2;FB2=(-t2+3)2,再根据DF=
+t-t)2+(-t2+3-3)2;FB2=(-t2+3)2,再根据DF=![]() FB,即可求得t;
FB,即可求得t;
②如图3所示,画出旋转后的图形,认真分析满足题意要求时,需要具备什么样的限制条件,然后根据限制条件列出不等式,求出的取值范围,确定限制条件是解题的关键
(1)由题意得AB的中点坐标为(![]() ,0),CD的中点坐标为(0,3),
,0),CD的中点坐标为(0,3),
分别代入y=ax2+b得:![]() ,解得
,解得![]() ,
,
∴y=x2+3.
(2)①D(![]() ,3),则平移后坐标为D(
,3),则平移后坐标为D(![]() +t,3),F(t,-t2+3);
+t,3),F(t,-t2+3);
DF2=(![]() +t-t)2+(-t2+3-3)2;FB2=(-t2+3)2
+t-t)2+(-t2+3-3)2;FB2=(-t2+3)2
DF=![]() FB,则(
FB,则(![]() +t-t)2+(-t2+3-3)2=7(-t2+3)2
+t-t)2+(-t2+3-3)2=7(-t2+3)2
解得:t2=2或5,则t=![]() 或t=
或t=![]() ;
;
②如图3所示,依题意作出旋转后的三角形△FE′C′,过C′作MN⊥x轴,分别交抛物线、x轴于点M、点N.
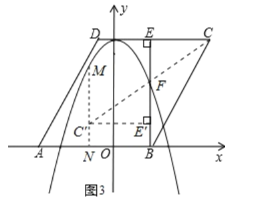
观察图形可知,欲使△FE′C′落在指定区域内,必须满足:EE′BE且MNC′N.
∵F(t,3t2),∴EF=3(3t2)=t2,∴EE′=2EF=2t2,
由EE′BE,得2t23,解得t![]() .
.
∵C′E′=CE=![]() ,∴C′点的横坐标为t
,∴C′点的横坐标为t![]() ,
,
∴MN=3(t![]() )2,又C′N=BE′=BEEE′=32t2
)2,又C′N=BE′=BEEE′=32t2
由MNC′N,得3(t![]() )232t2,解得t
)232t2,解得t![]()
![]() 或t
或t![]()
![]() (舍去).
(舍去).
∴t的取值范围为:![]()
![]() t
t![]() .
.

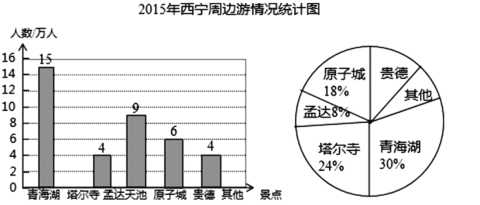
【题目】良好的饮食对学生的身体、智力发育和健康起到了极其重要的作用,荤菜中蛋白质、钙、磷及脂溶性维生素优于素食,而素食中不饱和脂肪酸、维生素和纤维素又优于荤食,只有荤食与素食适当搭配,才能强化初中生的身体素质.某校为了了解学生的体质健康状况,以便食堂为学生提供合理膳食,对本校七年级、八年级学生的体质健康状况进行了调查,过程如下:
收集数据:从七、八年级两个年级中各抽取15名学生,进行了体质健康测试,测试成绩(百分制)如下:
七年级:74 81 75 76 70 75 75 79 81 70 74 80 91 69 82
八年级:81 94 83 77 83 80 81 70 81 73 78 82 80 70 50
整理数据:
年级 | x<60 | 60≤x<80 | 80≤x<90 | 90≤x≤100 |
七年级 | 0 | 10 | 4 | 1 |
八年级 | 1 | 5 | 8 | 1 |
(说明:90分及以上为优秀,80~90分(不含90分)为良好,60~80分(不含80分)为及格,60分以下为不及格)
分析数据:
年级 | 平均数 | 中位数 | 众数 |
七年级 |
| 75 | 75 |
八年级 | 77.5 | 80 |
|
得出结论:
(2)可以推断出 年级学生的体质健康状况更好一些,并说明理由;
(3)若七年级共有300名学生,请估计七年级体质健康成绩优秀的学生人数.