题目内容
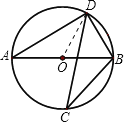
【题目】如图,若AB是⊙O的直径,CD是⊙O的弦,∠ABD=58°,则∠BCD=________.

【答案】32°
【解析】试题分析:根据圆周角定理求得∠AOD=2∠ABD=116°(同弧所对的圆周角是所对的圆心角的一半)、∠BOD=2∠BCD(同弧所对的圆周角是所对的圆心角的一半);根据平角是180°知∠BOD=180°﹣∠AOD,故∠BCD=32°.
解:连接OD.
∵AB是⊙0的直径,CD是⊙O的弦,∠ABD=58°,
∴∠AOD=2∠ABD=116°(同弧所对的圆周角是所对的圆心角的一半);
又∵∠BOD=180°﹣∠AOD,∠BOD=2∠BCD(同弧所对的圆周角是所对的圆心角的一半);
∴∠BCD=32°;
另法:∵AB为直径,
∴∠ADB=90°,
∵∠ABD=58°,
∴∠A=90°﹣58°=32°,
∵∠BCD和∠A都是BD所对圆周角,
∴∠BCD=32°.
故答案为:32°.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


