Question

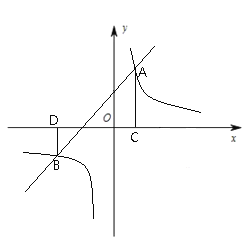
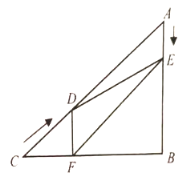
【题目】如图，在直角中，，，作的平分线交于点，在上取点，以点为圆心经过、两点画圆分别与、相交于点、（异于点）．

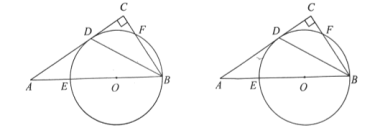
（1）求证：是的切线；

（2）若点恰好是的中点，求的长；

（3）若的长为．

①求的半径长；

②点关于轴对称后得到点，求与的面积之比．

Answer 1

【答案】（1）见解析；（2）；（3）①或；②或

【解析】

（1）连接DO，如图，先根据角平分线的定义以及平行线的性质，得出∠1=∠3，从而得到DO∥BC，再根据∠C=90°，可得出结果；

（2）连接FO，根据E为中点，可以得出，在Rt△AOD中，可以求出sinA的值，从而得出∠A的度数，再证明△BOF为等边三角形，从而得出∠BOF的度数，根据弧长公式可得出结果；

（3）①设圆的半径为r，过作于，则，四边形是矩形．再证明，得出，据此列方程求解；

②作出点F关于BD的对称点F′，连接DE，DF，DF′，FF′，再证明，最后根据相似三角形的面积比等于相似比的平方求解．

（1）证明：连结，

∵平分，∴，

∵，∴．∴．∴．

∵，∴．

∴是的切线．

（2）解：∵是中点，∴．

∴，∴，．

连接FO，

又BO=OF，∴△BOF为等边三角形，

∴．

∴．

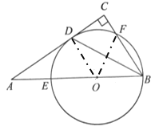
（3）解：①过作于，则，四边形是矩形．

设圆的半径为，则，．

∵，∴．

而，∴．

∴即，

解之得，．

②作出点F关于BD的对称点F′，连接FF′，DE，DF，DF′，

∵∠EBD=∠FBD，∴．

∵是直径，∴，

而、关于轴对称，∴，，DF=DF′，

∴DE∥FF′，DE=DF′，∠DEF′=∠DF′E，

∴，

∴.

当时，，，，

由①知，而，

∴.

又易得△BCD∽△BDE,∴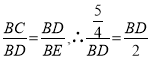，∴BD2=.

在Rt△BED中，DE2=BE2-BD2=4-=，∴DE==DF′.

∴与的面积比．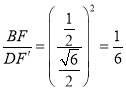

同理可得，当时，与的面积比．

∴与的面积比为或．