题目内容
如图,已知△OP1A1、△A1P2A2、△A2P3A3、……均为等腰直角三角形,直角顶点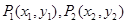 ……
…… 在函数
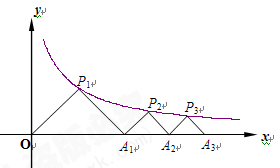
在函数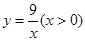 图象上,点A1、A2、 A3、……在x轴的正半轴上,则
图象上,点A1、A2、 A3、……在x轴的正半轴上,则 ……
……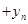 = .
= .
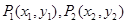 ……
……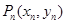 在函数
在函数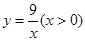 图象上,点A1、A2、 A3、……在x轴的正半轴上,则
图象上,点A1、A2、 A3、……在x轴的正半轴上,则 ……
…… = .
= .

解:如图,过点P1作P1M⊥x轴,
∵△OP1A1是等腰直角三角形,
∴P1M=OM=MA1,
设P1的坐标是(a,a),
把(a,a)代入解析式y=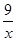 (x>0)中,得a=3,
(x>0)中,得a=3,
∴A1的坐标是(6,0),
又∵△P2A1A2是等腰直角三角形,
设P2的纵坐标是b,则P2的横坐标是6+b,
把(6+b,b)代入函数解析式得b= ,解得b=
,解得b= ,
,
∴A2的横坐标是6+2b=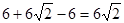 ,
,
同理可以得到A3的横坐标是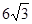 ,
,
An的横坐标是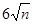 ,
,
根据等腰三角形的性质得到y1+y2+…yn等于An点横坐标的一半,
∴y1+y2+…yn=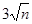 .
.
故答案为: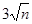 .
.
本题主要考查了反比例函数的综合应用,找出求P点坐标的规律,以这个规律为基础求出Pn的横坐标,进而求出An的横坐标的值,从而可得出所求的结果.
∵△OP1A1是等腰直角三角形,
∴P1M=OM=MA1,
设P1的坐标是(a,a),
把(a,a)代入解析式y=
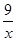 (x>0)中,得a=3,
(x>0)中,得a=3,∴A1的坐标是(6,0),
又∵△P2A1A2是等腰直角三角形,
设P2的纵坐标是b,则P2的横坐标是6+b,
把(6+b,b)代入函数解析式得b=
 ,解得b=
,解得b=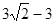 ,
,∴A2的横坐标是6+2b=
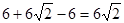 ,
,同理可以得到A3的横坐标是
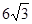 ,
,An的横坐标是
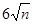 ,
,根据等腰三角形的性质得到y1+y2+…yn等于An点横坐标的一半,
∴y1+y2+…yn=
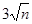 .
.故答案为:
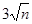 .
.本题主要考查了反比例函数的综合应用,找出求P点坐标的规律,以这个规律为基础求出Pn的横坐标,进而求出An的横坐标的值,从而可得出所求的结果.

练习册系列答案
相关题目
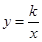 的图象经过点
的图象经过点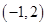 ,则
,则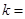 .
.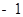 ),
),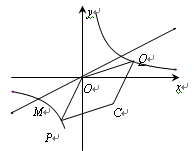
 的取值范围;
的取值范围; 中,一次函数
中,一次函数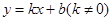 的图象与反比例函数
的图象与反比例函数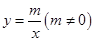 的图象交于二、四象限内的A、B两点,点B的坐标为(
的图象交于二、四象限内的A、B两点,点B的坐标为(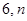 ).线段
).线段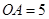 ,E为x轴负半轴上一点,且sin∠AOE=
,E为x轴负半轴上一点,且sin∠AOE=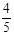 ,求该反比例函数和一次函数的解析式.
,求该反比例函数和一次函数的解析式.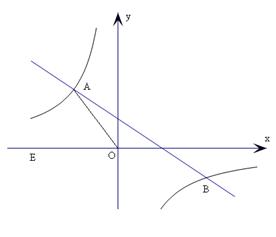
 中,已知反比例函数
中,已知反比例函数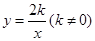 满足:当
满足:当 时,y随x的增大而减小。若该反比例函数的图象与直线
时,y随x的增大而减小。若该反比例函数的图象与直线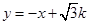 都经过点P,且
都经过点P,且 ,则实数k=_________.
,则实数k=_________.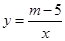 (m为常数)图象的一支.
(m为常数)图象的一支.
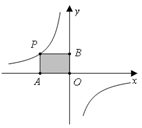
 图象在第一象限的交点为A(2,n),
图象在第一象限的交点为A(2,n),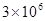 株郁金香为京城增添了亮丽的色彩.若这些郁金香平均每平方米种植的数量为
株郁金香为京城增添了亮丽的色彩.若这些郁金香平均每平方米种植的数量为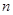 (单位:株/平方米),总种植面积为
(单位:株/平方米),总种植面积为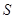 (单位:平方米),则
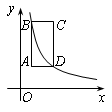
(单位:平方米),则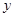 轴平行,顶点A的坐标为(1,2),点B、D在反比例函数
轴平行,顶点A的坐标为(1,2),点B、D在反比例函数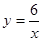 (
(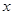 >0)的图象上,则点C的坐标为 ▲ .
>0)的图象上,则点C的坐标为 ▲ .