题目内容
在平面直角坐标系 中,已知反比例函数
中,已知反比例函数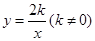 满足:当
满足:当 时,y随x的增大而减小。若该反比例函数的图象与直线
时,y随x的增大而减小。若该反比例函数的图象与直线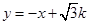 都经过点P,且
都经过点P,且 ,则实数k=_________.
,则实数k=_________.
 中,已知反比例函数
中,已知反比例函数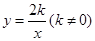 满足:当
满足:当 时,y随x的增大而减小。若该反比例函数的图象与直线
时,y随x的增大而减小。若该反比例函数的图象与直线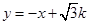 都经过点P,且
都经过点P,且 ,则实数k=_________.
,则实数k=_________.
设出P的坐标为(a,b),由P为两函数的交点,将P坐标代入反比例与直线解析式中,得到ab与a+b,在利用勾股定理表示出|OP|,代入|OP|= 中,利用完全平方公式变形,把表示出的ab与a+b代入,得到关于k的方程,求出方程的解即可得到k的值.
中,利用完全平方公式变形,把表示出的ab与a+b代入,得到关于k的方程,求出方程的解即可得到k的值.
解答:解:设P坐标为(a,b),代入反比例解析式得:ab=2k;代入直线解析式得:a+b= k,
k,
∵|OP|= ,即a2+b2=7,
,即a2+b2=7,
∴a2+b2=(a+b)2-2ab=3k2-4k=7,△=16+84=100>0,
分解因式得:(3k-7)(k+1)=0,
可得3k-7=0或k+1=0,
解得:k=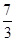 或k=-1(不合题意,舍去),
或k=-1(不合题意,舍去),
则实数k=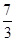 .
.
故答案为: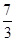
 中,利用完全平方公式变形,把表示出的ab与a+b代入,得到关于k的方程,求出方程的解即可得到k的值.
中,利用完全平方公式变形,把表示出的ab与a+b代入,得到关于k的方程,求出方程的解即可得到k的值.解答:解:设P坐标为(a,b),代入反比例解析式得:ab=2k;代入直线解析式得:a+b=
 k,
k,∵|OP|=
 ,即a2+b2=7,
,即a2+b2=7,∴a2+b2=(a+b)2-2ab=3k2-4k=7,△=16+84=100>0,
分解因式得:(3k-7)(k+1)=0,
可得3k-7=0或k+1=0,
解得:k=
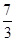 或k=-1(不合题意,舍去),
或k=-1(不合题意,舍去),则实数k=
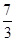 .
.故答案为:
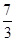

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
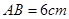 ,将直角顶点
,将直角顶点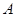 放在点(
放在点(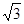 ,1)处,
,1)处,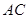 ∥
∥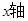 ,求经过点C的反比例函数的解析式.
,求经过点C的反比例函数的解析式.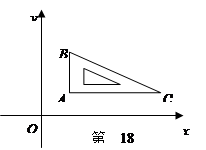
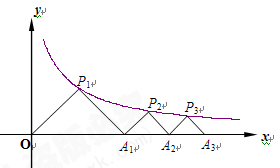
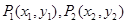 ……
……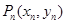 在函数
在函数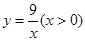 图象上,点A1、A2、 A3、……在x轴的正半轴上,则
图象上,点A1、A2、 A3、……在x轴的正半轴上,则 ……
……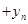 = .
= .
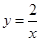 与
与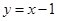 的图象的交点坐标为(
的图象的交点坐标为(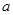 ,
,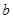 ),则
),则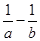 的值为__▲___.
的值为__▲___.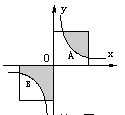
 的面积为9,点
的面积为9,点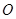 为坐标原点,点
为坐标原点,点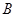 在函数
在函数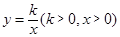 的图象上,点
的图象上,点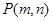 是函数
是函数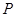 分别作
分别作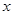 轴、
轴、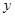 轴的垂线,垂足分别为
轴的垂线,垂足分别为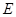 、
、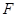 ,并设矩形
,并设矩形 和正方形
和正方形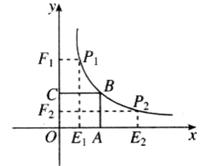
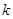 的值;
的值;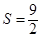 时,求
时,求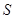 关于
关于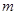 的函数关系式.
的函数关系式.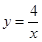 ,下列结论中,不正确的是 ( )
,下列结论中,不正确的是 ( )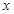 轴对称
轴对称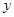 <4
<4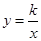 的图象经过点(-2,1),则k的值为_______.
的图象经过点(-2,1),则k的值为_______.