题目内容
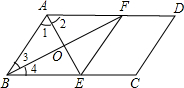
22、已知：如图所示，在△ABC和△DCB中，∠A=∠D=90°，AC与BD相交于点O，AC=DB．求证：△OBC为等腰三角形．分析：用HL证△ABC≌△DCB，得∠ACB=∠DBC，得OB=OC，得证．
解答：证明：∵在△ABC和△DCB中，∠A=∠D=90°，AC=DB．
∴△ABC≌△DCB（HL），
∴∠DBC=∠ACB，
即∠OBC=∠OCB，
∴OB=OC，
∴△OBC为等腰三角形．
∴△ABC≌△DCB（HL），
∴∠DBC=∠ACB，
即∠OBC=∠OCB，
∴OB=OC，
∴△OBC为等腰三角形．
点评：此题利用全等三角形的判定与性质，来求证等腰三角形的，关键是判定用HL证△ABC≌△DCB，是一道基础题．
练习册系列答案
相关题目
阅读下述说明过程，讨论完成下列问题：
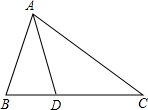已知：如图所示，在△ABC中，AB=AD=DC，∠BAD=26°，求∠B和∠C的度数．
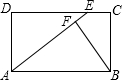已知：如图所示，在矩形ABCD中，E为DC上的一点，BF⊥AE于点F，且BF=BC，求证：AE=AB．
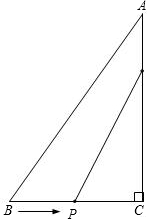同时出发，其中点P以1厘米/秒的速度沿着线段BC向点C运动，点Q以2厘米/秒的速度沿着线段CA向点A运动．
点M，连接DC．