��Ŀ����
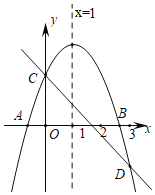
����Ŀ����ͼ��ֱ��l1��y��6x+6��x�ᡢy��ֱ���A��D���㣬ֱ��l2��y����x+3��x�ᡢy��ֱ���B��C���㣮
��1����ֱ��l2����һ��E��ʹ|AE��DE|��ֵ�����|AE��DE|�����ֵ��
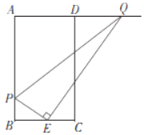
��2����ABΪ��������ABMN����C�ڱ�MN�ϣ�����P��B������������BM�����ƶ�������PAB����ֱ��PA�ĶԳơ�PAB'���Ƿ���ڵ�P��ʹ�á�PMB'��ֱ�������Σ������ڣ���ֱ��д�����з�������ĵ�P�����ꣿ�������ڣ���˵�����ɣ�
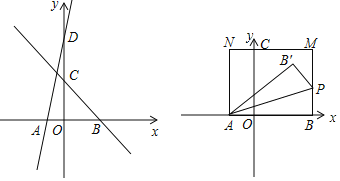
���𰸡���1��![]() ����2�����������ĵ�P������Ϊ��3��
����2�����������ĵ�P������Ϊ��3��![]() ����3��
����3��![]() ����
����
��������
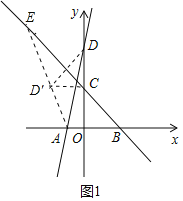
��1����ͼ1�У�����D����ֱ��y����x+3�ĶԳƵ�D�䣬����CD�䣬AD�䣬�ӳ�AD�佻ֱ��BC��E����E��Ϊ����֤����DCD���ǵ���ֱ�������������D������꼴�ɽ�����⣮
��2�����������Σ���ͼ2��1�У�����PB��M��90��ʱ��A��B�䣬M���ߣ���ͼ2��2�У�����PMB�䣽90��ʱ����B������MN�ϣ��ֱ����ù��ɶ��������������ε�������⼴�ɣ�
�⣺��1����ֱ��l1��y��6x+6��x�ᡢy��ֱ���A��D���㣬ֱ��l2��y����x+3��x�ᡢy��ֱ���B��C���㣬
��A����1��0����D��0��6����B��3��0����C��0��3����
��ͼ1�У�����D����ֱ��y����x+3�ĶԳƵ�D�䣬����CD�䣬AD�䣬�ӳ�AD�佻ֱ��BC��E����E��Ϊ����
��OC��3��OD��6��
��CD��3��
�ߡ�DCE����OCB����ECD�䣽45�㣬
���DCD�䣽90�䣬
��D�䣨��3��3����
��AD�䣽![]() ��
��
��|AE��DE|�����ֵ��AD�䣽![]() ��
��
��2����ͼ2��1�У�����PB��M��90��ʱ��A��B�䣬M���ߣ�
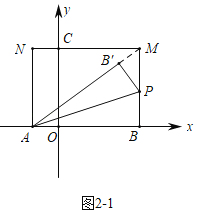
��Rt��ABM�У��ߡ�ABM��90�㣬AB��4��BM��3��
��AB��![]() ��
��
��AB��AB�䣽4��
��MB�䣽5��4��1����PB��PB�䣽x��
��Rt��PMB��������3��x��2��x2+12��
��ã�x��![]() ��
��
��P��3��![]() ����
����
��ͼ2��2�У�����PMB�䣽90��ʱ����B������MN�ϣ�
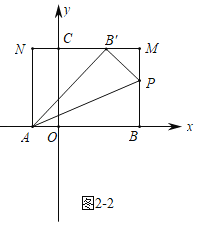
��Rt��ANB���У��ߡ�N��90�㣬AB�䣽AB��4��AN��3��
��NB�䣽![]() ��
��
�ߡ�AB��P����M����N��90�㣬
���NAB��+��AB��N��90�㣬��AB��N+��PB��M��90�㣬
���NAB�䣽��MB��P��
���ANB��ס�B��MP��
��![]() ��
��
��![]() ��
��
��PB�䣽![]() ��
��
��PB��PB�䣽![]() ��
��
��P��3��![]() ����
����
�������������������ĵ�P������Ϊ��3��![]() ����3��
����3��![]() ����
����

����Ŀ��Ϊ���ﴫͳ�Ļ���ijУ��չ�������о����Ļ����Ķ��������������Ϊ�˽��ߡ����꼶ѧ��(�ߡ����꼶����600��ѧ��)���Ķ�Ч������У�����˾����Ļ�֪ʶ�������ִ������꼶�������ȡ20��ѧ���ľ����ɼ�(�ٷ���)���з������������£�
�ռ����ݣ�
���꼶��79��85��73��80��75��76��87��70��75��94��75��79��81��71��75��80��86��59��83��77��
���꼶��92��74��87��82��72��81��94��83��77��83��80��81��71��81��72��77��82��80��70��41��
�������ݣ�
|
|
|
|
|
| |
���꼶 | 0 | 1 | 0 | a | 7 | 1 |
���꼶 | 1 | 0 | 0 | 7 | b | 2 |
�������ݣ�
ƽ���� | ���� | ��λ�� | |
���꼶 | 78 | 75 |
|
���꼶 | 78 |
| 80.5 |
Ӧ�����ݣ�
(1)���ϱ���գ�a= ��b= ��c= ��d= ��
(2)���Ƹ�У�ߡ��������꼶ѧ���ڱ��ξ����гɼ���90�����ϵĹ��ж����ˣ�
(3)����Ϊ�ĸ��꼶��ѧ���Ծ����Ļ�֪ʶ���յ�����ˮƽ�Ϻã���˵�����ɣ�