题目内容
【题目】乘法公式的探究及应用.
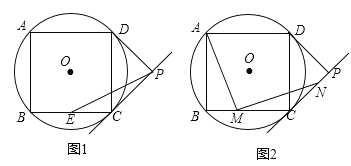
数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片边长为a的正方形,B种纸片是边长为b的正方形,C种纸片长为a、宽为b的长方形,并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
(1)请用两种不同的方法求图2大正方形的面积.
方法1:______;方法2:______.
(2)观察图2,请你写出下列三个代数式:(a+b)2,a2+b2,ab之间的等量关系.______;
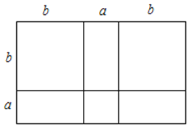
(3)类似的,请你用图1中的三种纸片拼一个图形验证:
(a+b)(a+2b)=a2+3ab+2b2
(4)根据(2)题中的等量关系,解决如下问题:
①已知:a+b=5,a2+b2=11,求ab的值;
②已知(x-2016)2+(x-2018)2=34,求(x-2017)2的值.

【答案】(1) (a+b)2;a2+b2+2ab;(2)(a+b)2=a2+2ab+b2;(3)见解析;(4)①7;②16.
【解析】
(1)第一种方法:直接用正方形的面积公式求解;第二种方法将其看做是一个两个正方形和两个长方形,分别求出面积再求和即可.
(2)依据(1)中的代数式,即可得到所求的关系;
(3)画出长为a+2b,宽为a+b的长方形,即可完成验证;
(4)①依据a+b=5,可得(a+b)2=25,进而得出a2+b2+2ab=25,再将a2+b2=11,即可得到ab=7;②设x-2017=a,则x-2016=a+1,x-2018=a-1,依据(x-2016)2+(x-2018)2=34,即可得到∴(a+1)2+(a-1)2=34,然后化简得a2=16,即可完成解答.
解:(1)图2大正方形的面积=(a+b)2;图2大正方形的面积=a2+b2+2ab;
故答案为:(a+b)2;a2+b2+2ab;
(2)由题可得(a+b)2,a2+b2,ab之间的等量关系为:(a+b)2=a2+2ab+b2;
故答案为:(a+b)2=a2+2ab+b2;
(3)如图所示,
(4)①∵a+b=5,
∴(a+b)2=25,即a2+b2+2ab=25,
又∵a2+b2=11,
∴ab=7;
②设x-2017=a,则x-2016=a+1,x-2018=a-1,
∵(x-2016)2+(x-2018)2=34,
∴(a+1)2+(a-1)2=34,
∴a2+2a+1+a2-2a+1=34,
∴2a2+2=34,
∴2a2=32,
∴a2=16,
即(x-2017)2=16.

 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案【题目】某商场计划经销A、B两种新型节能台灯共50盏,这两种台灯的进价、售价如下表所示.
价格/类型 | A型 | B型 |
进价(元/盏) | 40 | 65 |
售价(元/盏) | 60 | 100 |
(1)若该商场购进这批台灯共用去2500元,问这两种台灯各购进多少盏?
(2)在每种台灯销售利润不变的情况下,若该商场销售这批台灯的总利润不少于1400元,问至少需购进B种台灯多少盏?