题目内容
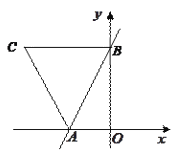
【题目】如图，AD是∠BAC平分线，点E在AB上，且AE=AC，EF∥BC交AC于点F，AD与CE交于点G，与EF交于点H．
（1）证明：AD垂直平分CE；
（2）若∠BCE=40°，求∠EHD的度数．
【答案】(1)见解析；（2）50°．
【解析】
(1)根据等腰三角形三线合一的性质可得出结论；(2)由(1)可知点D为CE垂直平分线上的点，则CD=DE，∠DCE=∠DEC.由EF∥BC，可得EG平分∠DEF；由EG⊥AD，可证∠EDH=∠EHD，根据内角和定理，即可得出结论.
解：(1)∵AE=AC，AD是∠BAC平分线，
∴AD垂直平分CE；
(2)由(1)可知点D为CE垂直平分线上的点，
∴CD=DE，
∴∠DCE=∠DEC．
∵EF∥BC，
∴∠DCE=∠CEF=∠DEC，
∴EG平分∠DEF．
∵EG⊥AD，EG=EG，
∴△DEG≌△HEG(ASA),
∴△DEH是等腰三角形，且ED=EH，
∴∠EDH=∠EHD，
∵∠BCE=40°，
∴∠DEH=2∠BCE=80°，
∴∠EHD=
(180°﹣80°)=50°．
练习册系列答案
相关题目
【题目】为了解某校学生的身高情况，随机抽取该校男生、女生进行抽样调查．已知抽取的样本中，男生、女生的人数相同，利用所得数据绘制如下统计图表： 身高情况分组表（单位：cm）
组别 | 身高 |
A | x＜155 |
B | 155≤x＜160 |
C | 160≤x＜165 |
D | 165≤x＜170 |
E | x≥170 |
根据图表提供的信息，回答下列问题：
（1）样本中，男生的身高众数在组，中位数在组；
（2）样本中，女生身高在E组的人数有人；
（3）已知该校共有男生400人，女生380人，请估计身高在160≤x＜170之间的学生约有多少人？
