题目内容
【题目】(10分)开学初,小明到文具批发部一次性购买某种笔记本,该文具批发部规定:这种笔记本售价y(元/本)与购买数量x(本)之间的函数关系如图所示.
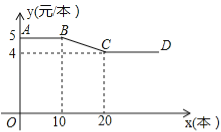
(1)图中线段AB所表示的实际意义是 ;
(2)请直接写出y与x之间的函数关系式;
(3)已知该文具批发部这种笔记本的进价是3元/本,若小明购买此种笔记本超过10本但不超过20本,那么小明购买多少本时,该文具批发部在这次买卖中所获的利润W(元)最大?最大利润是多少?
【答案】(1)购买不超过10本此种笔记本时售价为5元/本.(2)①当0<x≤10时,y=5;②当10<x≤20时,y=﹣0.1x+6;③当20<x时,y=4.(3)当小明购买15本时,该文具批发部在这次买卖中所获的利润最大,最大利润是22.5元.
【解析】
试题(1)观察一次函数图象可知线段AB与x轴平行,即可得出线段AB所表示的实际意义是:购买不超过10本此种笔记本时售价为5元/本;(2)观察一次函数图象可知,图象分三段,因此y与x之间的函数关系式分三种情况,①当0<x≤10时,②当10<x≤20时,③当x>20时,根据这三种情况分别求出y与x之间的函数关系式即可;(3)根据题意求出W与x之间的关系式,再利用二次函数的性质即可求解.
试题解析: 解:(1)图中线段AB所表示的实际意义是:购买不超过10本此种笔记本时售价为5元/本.
(2)①当0<x≤10时,
y与x之间的函数关系式y=5,
②当10<x≤20时,
设=kx+b把B(10,5),C(20,4)代入得![]() ,
,
解得![]() .
.
所以y与x之间的函数关系式y=﹣0.1x+6.
③当x>20时,y与x之间的函数关系式为:y=4.
(3)W=(﹣0.1x+6﹣3)x=﹣0.1×(x﹣15)2+22.5.
答:当小明购买15本时,该文具批发部在这次买卖中所获的利润最大,最大利润是22.5元.

 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案