Ő‚ńŅńŕ»›
°ĺŐ‚ńŅ°Ņ◊ŘļŌ”Ž Ķľý£ļ
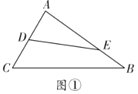
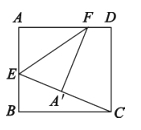
∂Į ÷≤Ŕ◊ų£ļ»ÁÕľ1£¨ňńĪŖ–ő![]() «“Ľ’Ňĺō–ő÷Ĺ∆¨£¨
«“Ľ’Ňĺō–ő÷Ĺ∆¨£¨![]() £¨
£¨![]() £¨Ķ„
£¨Ķ„![]() £¨
£¨![]() ∑÷Īū‘ŕ
∑÷Īū‘ŕ![]() £¨
£¨![]() ĪŖ…Ō£¨«“
ĪŖ…Ō£¨«“![]() £¨Ń¨Ĺ”
£¨Ń¨Ĺ”![]() £¨
£¨![]() .Ĺę
.Ĺę![]() £¨
£¨![]() ∑÷Īū—ō
∑÷Īū—ō![]() £¨
£¨![]() ’ŘĶĢ£¨Ķ„
’ŘĶĢ£¨Ķ„![]() £¨
£¨![]() ∑÷Īū¬š‘ŕĶ„
∑÷Īū¬š‘ŕĶ„![]() £¨
£¨![]() ī¶.
ī¶.
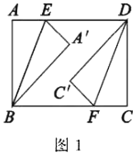
ŐĹĺŅ’Ļ ĺ£ļ
£®1£©°įŅŐŅŗ–°◊ť°Ī∑ĘŌ÷£ļ![]() £¨«“
£¨«“![]() £¨≤Ę’Ļ ĺŃň»ÁŌ¬Ķń÷§√ųĻż≥Ő.
£¨≤Ę’Ļ ĺŃň»ÁŌ¬Ķń÷§√ųĻż≥Ő.
÷§√ų£ļ‘ŕĺō–ő![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() £¨
£¨![]() .
.
”÷°Ŗ![]() £¨
£¨
°ŗ![]() .
.
°ŗ![]() £¨
£¨![]() .
.
°Ŗ![]() £¨
£¨
°ŗ![]() .£®“ņĺ›1£©
.£®“ņĺ›1£©
°ŗ![]() .
.
°ŗ![]() .£®“ņĺ›2£©
.£®“ņĺ›2£©
∑īňľĹĽŃų£ļĘŔ…Ō Ų÷§√ųĻż≥Ő÷–Ķń°į“ņĺ›1°Ī”Ž°į“ņĺ›2°Ī∑÷Īū÷ł ≤√ī£Ņ
Ęŕ°į«ŕ∑‹–°◊ť°Ī»Ōő™£ļĽĻŅ…“‘Õ®Ļż÷§√ųňńĪŖ–ő![]() «∆Ĺ––ňńĪŖ–őĽŮ÷§£¨«Žń„łýĺ›°į«ŕ∑‹–°◊ť°ĪĶń÷§√ųňľ¬∑–ī≥Ų÷§√ųĻż≥Ő.
«∆Ĺ––ňńĪŖ–őĽŮ÷§£¨«Žń„łýĺ›°į«ŕ∑‹–°◊ť°ĪĶń÷§√ųňľ¬∑–ī≥Ų÷§√ųĻż≥Ő.
≤¬ŌŽ÷§√ų£ļ
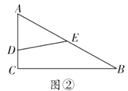
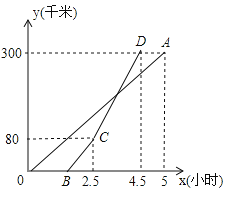
£®2£©»ÁÕľ2£¨’ŘĶĢĻż≥Ő÷–£¨ĶĪĶ„![]() £¨
£¨![]() ‘ŕ÷ĪŌŖ
‘ŕ÷ĪŌŖ![]() ĶńÕ¨≤ŗ Ī£¨—”≥§
ĶńÕ¨≤ŗ Ī£¨—”≥§![]() ĹĽ
ĹĽ![]() ”ŕĶ„
”ŕĶ„![]() £¨—”≥§
£¨—”≥§![]() ĹĽ
ĹĽ![]() ”ŕĶ„
”ŕĶ„![]() £¨‘ÚňńĪŖ–ő
£¨‘ÚňńĪŖ–ő![]() « ≤√īŐō ‚ňńĪŖ–ő£Ņ«ŽňĶ√ųņŪ”….
« ≤√īŐō ‚ňńĪŖ–ő£Ņ«ŽňĶ√ųņŪ”….
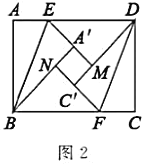
Ń™ŌŽÕōĻ„£ļ
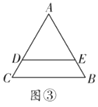
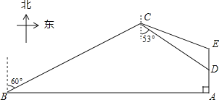
£®3£©»ÁÕľ3£¨Ń¨Ĺ”![]() £¨
£¨![]() £¨
£¨![]() .
.

ĘŔĶĪ![]() Ī£¨
Ī£¨![]() Ķń≥§ő™________£Ľ
Ķń≥§ő™________£Ľ
Ęŕ![]() Ķń≥§”–◊Óīů÷Ķ¬ū£Ņ»Ű”–£¨«Žń„÷ĪĹ”–ī≥Ų
Ķń≥§”–◊Óīů÷Ķ¬ū£Ņ»Ű”–£¨«Žń„÷ĪĹ”–ī≥Ų![]() ≥§Ķń◊Óīů÷ĶļÕīň ĪňńĪŖ–ő
≥§Ķń◊Óīů÷ĶļÕīň ĪňńĪŖ–ő![]() Ķń–ő◊ī£Ľ»Ű√Ľ”–£¨«ŽňĶ√ųņŪ”….
Ķń–ő◊ī£Ľ»Ű√Ľ”–£¨«ŽňĶ√ųņŪ”….
°ĺīūįł°Ņ£®1£©ĘŔľŻĹ‚őŲĘྯłőŲ£Ľ£®2£©ĺō–ő£¨ņŪ”…ľŻĹ‚őŲ£Ľ£®3£©ĘŔ![]() Ęŕ”–£Ľ
Ęŕ”–£Ľ![]() £ĽŃ‚–ő
£ĽŃ‚–ő
°ĺĹ‚őŲ°Ņ
£®1£©ĘŔłýĺ›∆Ĺ––ŌŖĶńŇ–∂®”Ž–‘÷ ľīŅ…Ķ√Ĺ‚£Ľ
Ęŕ”…ĺō–őĶń–‘÷ ĹÝ––Ķ»ŃŅ◊™ĽĽĶ√≥Ų![]() £¨ľīŅ…Ň–∂®ňńĪŖ–ő
£¨ľīŅ…Ň–∂®ňńĪŖ–ő![]() «∆Ĺ––ňńĪŖ–ő£¨ľīŅ…Ķ√÷§£Ľ
«∆Ĺ––ňńĪŖ–ő£¨ľīŅ…Ķ√÷§£Ľ
£®2£© ◊Ō»”…∂‘’ŘĶń–‘÷ Ķ√≥Ų![]() £¨
£¨![]() £¨»ĽļůņŻ”√
£¨»ĽļůņŻ”√![]() £¨ĹÝ––Ķ»ŃŅ◊™ĽĽ£¨Ķ√≥Ų
£¨ĹÝ––Ķ»ŃŅ◊™ĽĽ£¨Ķ√≥Ų![]() £¨ľīŅ…Ň–∂®ňńĪŖ–ő
£¨ľīŅ…Ň–∂®ňńĪŖ–ő![]() «ĺō–ő£Ľ
«ĺō–ő£Ľ
£®3£©ĘŔ—”≥§C°šA°šĹĽAD”ŕG£¨A°šC°šĹĽBC”ŕH£¨ņŻ”√°ųA°šGE°’°ųC°šHF£¨Ķ√≥ŲAG=BH=4£¨‘ŔņŻ”√ĻīĻ…∂®ņŪĻĻĹ®∑Ĺ≥Ő£¨ľīŅ…Ķ√≥ŲAE£Ľ
ĘŕĶĪ![]() °ÕBD Ī£¨
°ÕBD Ī£¨![]() Ķń≥§”–◊Óīů÷Ķ£¨ņŻ”√Ń‚–őĶń–‘÷ “‘ľįĻīĻ…∂®ņŪľīŅ…Ķ√Ĺ‚.
Ķń≥§”–◊Óīů÷Ķ£¨ņŻ”√Ń‚–őĶń–‘÷ “‘ľįĻīĻ…∂®ņŪľīŅ…Ķ√Ĺ‚.
£®1£©ĘŔ°į“ņĺ›1°Ī÷łŃĹ÷ĪŌŖ∆Ĺ––£¨ńŕīŪĹ«ŌŗĶ»£Ľ
°į“ņĺ›2°Ī÷łÕ¨őĽĹ«ŌŗĶ»£¨ŃĹ÷ĪŌŖ∆Ĺ––.
Ęŕ÷§√ų£ļ‘ŕĺō–ő![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() .
.
”÷°Ŗ![]() £¨
£¨
°ŗ![]() £¨ľī
£¨ľī![]() .
.
°ŗňńĪŖ–ő![]() «∆Ĺ––ňńĪŖ–ő.
«∆Ĺ––ňńĪŖ–ő.
°ŗ![]() £¨«“
£¨«“![]() .
.
£®2£©ňńĪŖ–ő![]() «ĺō–ő£¨
«ĺō–ő£¨
—”≥§![]() £¨ĹĽ
£¨ĹĽ![]() ”ŕĶ„
”ŕĶ„![]() £¨»ÁŌ¬Õľ.
£¨»ÁŌ¬Õľ.
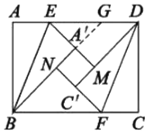
”…∂‘’ŘŅ…÷™£¨![]() .
.
°Ŗ![]() £¨
£¨
°ŗ![]() .
.
Õ¨ņŪ£¨![]() .
.
”…£®1£©Ķ√£¨![]() £¨
£¨
°ŗ![]() .
.
”…∂‘’ŘŅ…÷™£¨![]() £¨
£¨![]() .
.
°ŗ![]()
‘ŕ![]() ÷–£¨
÷–£¨![]() .
.
‘ŕĺō–ő![]() ÷–£¨
÷–£¨![]() £¨ľī
£¨ľī![]() .
.
°ŗ![]() .
.
°ŗ![]() .
.
°ŗ![]() .
.
°ŗ![]() .
.
°ŗňńĪŖ–ő![]() «ĺō–ő.
«ĺō–ő.
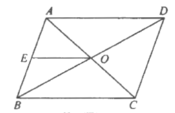
£®3£©ĘŔ—”≥§C°šA°šĹĽAD”ŕG£¨A°šC°šĹĽBC”ŕH£¨»ÁÕľňý ĺ£ļ
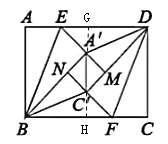
°Ŗ![]()
°ŗGH°őAB
°ŗ°ŌA°šGE=°ŌC°šHF=90°„£¨AG=BH
°Ŗ°ŌEA°šG=°ŌFC°šH£¨A°šE=C°šF
°ŗ°ųA°šGE°’°ųC°šHF
°ŗEG=FH
°ŖAE=CF
°ŗAG=CH
°ŗAG=BH=4
°ŗ![]()
°ŗ![]()
…ŤAE=x£¨‘ÚEG=4-x£¨
‘ŕRt°ųA°šEG÷–£¨![]()
ľī![]()
Ĺ‚Ķ√![]() £¨ľīAE=
£¨ľīAE=![]() £Ľ
£Ľ
ĘŕĶĪ![]() °ÕBD Ī£¨
°ÕBD Ī£¨![]() Ķń≥§”–◊Óīů÷Ķ£¨◊Óīů÷Ķő™
Ķń≥§”–◊Óīů÷Ķ£¨◊Óīů÷Ķő™![]()
![]() £¨īň ĪňńĪŖ–ő
£¨īň ĪňńĪŖ–ő![]() «Ń‚–ő.
«Ń‚–ő.

 ĺŔ“Ľ∑ī»żÕ¨≤Ĺ«…Ĺ≤ĺęŃ∑ŌĶŃ–īūįł
ĺŔ“Ľ∑ī»żÕ¨≤Ĺ«…Ĺ≤ĺęŃ∑ŌĶŃ–īūįł Ņŕň„”Ž”¶”√Ő‚Ņ®ŌĶŃ–īūįł
Ņŕň„”Ž”¶”√Ő‚Ņ®ŌĶŃ–īūįł √Ż ¶Ķ„ĺ¶◊÷ī ĺš∂ő∆™ŌĶŃ–īūįł
√Ż ¶Ķ„ĺ¶◊÷ī ĺš∂ő∆™ŌĶŃ–īūįł