Question

【题目】如图，在四边形ABCD中，AB∥CD，点E、F在对角线AC上，且∠ABF＝∠CDE，AE＝CF．

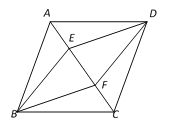
（1）求证：△ABF≌△CDE；

（2）当四边形ABCD的边AB、AD满足什么条件时，四边形BFDE是菱形?说明理由．

Answer 1

【答案】（1）证明见解析（2）当四边形ABCD满足AB＝AD时，四边形BEDF是菱形．

【解析】试题分析：（1）根据平行线的性质，可求得∠BAC=∠DCA，然后根据等量代换可得AF=CE，最后可根据“AAS”可证；

（2）连接BD交AC于点O，由（1）的结论的到B＝CD，BF＝DE，∠AFB＝∠CED,然后根据一边平行且相等的四边形是平行四边形，可证四边形ABCD是平行四边形，进而得到菱形ABCD，再根据菱形的判定证得四边形BEDF是菱形即可.

试题解析：（1）∵AB∥CD，∴∠BAC＝∠DCA．

∵AE＝CF，∴AE＋EF＝CF＋EF，即AF＝CE．

又∵∠ABF＝∠CDE，

∴△ABF≌△CDE．

（2）当四边形ABCD满足AB＝AD时，四边形BEDF是菱形．

连接BD交AC于点O，

由（1）△ABF≌△CDE 得AB＝CD，BF＝DE，∠AFB＝∠CED,∴BF∥DE．

∵AB∥CD，AB＝CD，∴四边形ABCD是平行四边形．

又∵AB＝AD，∴□ABCD是菱形．∴BD⊥AC．

∵BF＝DE，BF∥DE，∴四边形BEDF是平行四边形，

∴□BEDF是菱形．