题目内容
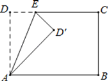
【题目】如图①,在4×8的网格纸中,每个小正方形的边长都为1,动点P、Q分别从点D、A同时出发向右移动,点P的运动速度为每秒2个单位,点Q的运动速度为每秒1个单位,当点P运动到点C时,两个点都停止运动,设运动时间为t(0<t<4).


(1)请在4×8的网格纸图①中画出t为3秒时的线段PQ.并求其长度;
(2)若M是BC的中点,记△PQM的面积为S,请用含有t的代数式来表示S;
(3)当t为多少时,△PQB是以PQ为腰的等腰三角形?
【答案】(1)图见解析,PQ=5;(2)![]() ;(3)t=3 或
;(3)t=3 或![]() 时,△PQB是以PQ为腰的等腰三角形.
时,△PQB是以PQ为腰的等腰三角形.
【解析】
根据点P的运动速度为每秒2个单位,点Q的运动速度为每秒1个单位可知,当t=3秒时,DP=6,AQ=3即可画出线段PQ;
(2)利用割补法求三角形面积;
(3)设时间为t,则在t秒钟,P运动了2t个格,Q运动了t个格,分情况 PQ=BQ和PQ=BP,然后根据勾股定理列出关于t的方程,解得t即可.
如图所示:

由勾股定理得PQ=![]() =5;
=5;
(2)∵M是BC的中点
∴CM=BM
![]()
![]()
(3)设时间为t,则在t秒钟,P运动了2t格,Q运动了t格
当PQ=BQ时,即(2t﹣t)2+42=(8﹣t)2,解得t=3(秒).
当PQ=BP时,![]() (8﹣t)=8﹣2t,解得:t=
(8﹣t)=8﹣2t,解得:t=![]() ∴综上,t=3 或
∴综上,t=3 或![]() 时,△PQB是以PQ为腰的等腰三角形.
时,△PQB是以PQ为腰的等腰三角形.

 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案【题目】(10分)学校组织学生参加综合实践活动,他们参与了某种品牌运动鞋的销售工作,已知该运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如下表所示:
第1天 | 第2天 | 第3天 | 第4天 | |
售价x(元/双) | 150 | 200 | 250 | 300 |
销售量y(双) | 40 | 30 | 24 | 20 |
(1)观察表中数据,x,y满足什么函数关系?请求出这个函数关系式;
(2)若商场计划每天的销售利润为3000元,则其单价定为多少元?