Question

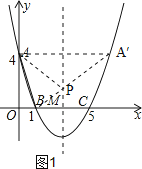
【题目】如图，在直角坐标系中，抛物线经过点A（0，4），B（1，0），C（5，0），其对称轴与x轴相交于点M．

（1）求抛物线的解析式和对称轴；
（2）在抛物线的对称轴上是否存在一点P，使△PAB的周长最小？若存在，请求出点P的坐标；若不存在，请说明理由；
（3）连接AC，在直线AC的下方的抛物线上，是否存在一点N，使△NAC的面积最大？若存在，请求出点N的坐标；若不存在，请说明理由．

Answer 1

【答案】
（1）

【解答】解：根据已知条件可设抛物线的解析式为y=a（x﹣1）（x﹣5），

把点A（0，4）代入上式得：a=，

∴y=（x﹣1）（x﹣5）=x2﹣x+4=（x﹣3）2﹣，

∴抛物线的对称轴是：x=3；

（2）

P点坐标为（3，）．

理由如下：

∵点A（0，4），抛物线的对称轴是x=3，

∴点A关于对称轴的对称点A′的坐标为（6，4）

如图1，连接BA′交对称轴于点P，连接AP，此时△PAB的周长最小．

设直线BA′的解析式为y=kx+b，

把A′（6，4），B（1，0）代入得，

解得，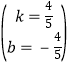

∴y=x﹣，

∵点P的横坐标为3，

∴y=×3﹣=，

∴P（3，）．

（3）

在直线AC的下方的抛物线上存在点N，使△NAC面积最大．

设N点的横坐标为t，此时点N（t，t2﹣t+4）（0＜t＜5），

如图2，过点N作NG∥y轴交AC于G；作AD⊥NG于D，

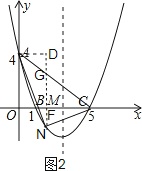
由点A（0，4）和点C（5，0）可求出直线AC的解析式为：y=﹣x+4，

把x=t代入得：y=﹣t+4，则G（t，﹣t+4），

此时：NG=﹣t+4﹣（t2﹣t+4）=﹣t2+4t，

∵AD+CF=CO=5，

∴S△ACN=S△ANG+S△CGN=AD×NG+NG×CF=NGOC=×（﹣t2+4t）×5=﹣2t2+10t=﹣2（t﹣）2+，

∴当t=时，△CAN面积的最大值为，

由t=，得：y=t2﹣t+4=﹣3，

∴N（，﹣3）．

【解析】（1）抛物线经过点A（0，4），B（1，0），C（5，0），可利用两点式法设抛物线的解析式为y=a（x﹣1）（x﹣5），代入A（0，4）即可求得函数的解析式，则可求得抛物线的对称轴；
（2）点A关于对称轴的对称点A′的坐标为（6，4），连接BA′交对称轴于点P，连接AP，此时△PAB的周长最小，可求出直线BA′的解析式，即可得出点P的坐标．
（3）在直线AC的下方的抛物线上存在点N，使△NAC面积最大．设N点的横坐标为t，此时点N（t，t2﹣t+4）（0＜t＜5），再求得直线AC的解析式，即可求得NG的长与△ACN的面积，由二次函数最大值的问题即可求得答案．