题目内容
【题目】如图，四边形ABCD中，∠BAD=∠ADC=90°，AB=AD= 
，CD= 
，点P是四边形ABCD四条边上的一个动点，若P到BD的距离为 
，则满足条件的点P有个．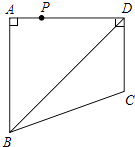 
【答案】2
【解析】解：过点A作AE⊥BD于E，过点C作CF⊥BD于F，
∵∠BAD=∠ADC=90°，AB=AD= 
，CD=2 
，
∴∠ABD=∠ADB=45°，
∴∠CDF=90°﹣∠ADB=45°，
∵sin∠ABD= 
，
∴AE=ABsin∠ABD=3 sin45°=3＞ 
，
CF=2＜ ，
所以在AB和AD边上有符合P到BD的距离为 的点2个，
所以答案是：2．
【考点精析】利用点到直线的距离对题目进行判断即可得到答案，需要熟知从直线外一点到这条直线的垂线段的长度叫做点到直线的距离．
练习册系列答案
相关题目
【题目】下面是某同学对多项式（x2－4x+2）（x2－4x+6）+4进行因式分解的过程．
解：设x2－4x=y
原式=（y+2）（y+6）+4 （第一步）
=y2+8y+16 （第二步）
=（y+4）2（第三步）
=（x2－4x+4）2（第四步）
回答下列问题：
（1）该同学第二步到第三步运用了因式分解的_______．
A．提取公因式 |
B．平方差公式 |
C．两数和的完全平方公式 |
D．两数差的完全平方公式 |
（2）该同学因式分解的结果是否彻底？________．（填“彻底”或“不彻底”）若不彻底，请直接写出因式分解的最后结果_________ ．
（3）请你模仿以上方法尝试对多项式（x2－2x）（x2－2x+2）+1进行因式分解．
