题目内容
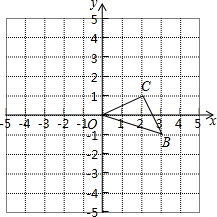 如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1)、(2,1).
如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1)、(2,1).(1)以0点为位似中心在y轴的左侧将△OBC放大到两倍(即新图与原图的相似比为2),画出图形并写出点 B1、C1的坐标;
(2)将△BOC绕O点逆时针旋转90°,画出旋转后的图形△OB2C2,并求出B点所经过的路线长.
考点:作图-位似变换,弧长的计算,作图-旋转变换
专题:作图题
分析:(1)利用位似图形的性质得出B,C点对应点 B1、C1的坐标即可;
(2)根据网格结构找出点C、B绕点O逆时针旋转90°后的对应点C2、B2的位置,然后顺次连接即可,再根据弧长公式列式计算即可得解.
(2)根据网格结构找出点C、B绕点O逆时针旋转90°后的对应点C2、B2的位置,然后顺次连接即可,再根据弧长公式列式计算即可得解.
解答: 解:(1)如图所示:B1、C1的坐标分别为:(-3,2),(-4,-2);
解:(1)如图所示:B1、C1的坐标分别为:(-3,2),(-4,-2);
(2)如图所示:△OB2C2即为所求,B点所经过的路线长为:
=
.
 解:(1)如图所示:B1、C1的坐标分别为:(-3,2),(-4,-2);
解:(1)如图所示:B1、C1的坐标分别为:(-3,2),(-4,-2);(2)如图所示:△OB2C2即为所求,B点所经过的路线长为:
90π×
| ||
| 180 |
| ||
| 2 |
点评:本题考查了利用旋转变换作图,弧长的计算,熟练掌握网格结构,准确找出对应点的位置是解题的关键.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
 如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于N,连接BM,DN.
如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于N,连接BM,DN.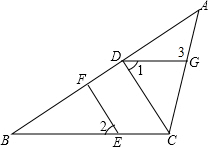 如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F. 已知:如图,矩形ABCD的对角线相交于点O,DE∥AC,AE∥DB,AE、DE交于点E.求证:四边形DOAE是菱形.
已知:如图,矩形ABCD的对角线相交于点O,DE∥AC,AE∥DB,AE、DE交于点E.求证:四边形DOAE是菱形.