题目内容
在等腰梯形ABCD中，AB∥DC，AB=DC=CB=3cm，求∠A的度数及梯形周长．
考点：等腰梯形的性质
专题：几何图形问题
分析：过B作BE∥AD交DC于E，利用等腰梯形的性质和已知条件可证明△BEC是等边三角形，进而得到∠C=60°，所以∠A的度数可求出，在求出DCA的长即可得到梯形的周长．
解答：
解：过B作BE∥AD交DC于E，
∵AB∥DC，
∴四边形ABED是平行四边形，
∴AD=BE，
∵AD=BC，
∴DE=BC，
∵AB=DC=CB=3cm，
∴BE=CE=BC，
∴△BEC是等边三角形，
∴∠C=60°，
∴∠D=60°，
∴∠A=120°，
∵DC=DE+CE=2×3=6cm，
∴梯形周长=3+3+3+6=15cm．
解：过B作BE∥AD交DC于E，∵AB∥DC，
∴四边形ABED是平行四边形，
∴AD=BE，
∵AD=BC，
∴DE=BC，
∵AB=DC=CB=3cm，
∴BE=CE=BC，
∴△BEC是等边三角形，
∴∠C=60°，
∴∠D=60°，
∴∠A=120°，
∵DC=DE+CE=2×3=6cm，
∴梯形周长=3+3+3+6=15cm．
点评：本题主要考查对等边三角形的性质和判定，平行四边形的性质和判定，等腰三角形的性质，等腰梯形的性质等知识点的理解和掌握，能综合运用这些性质进行推理是解此题的关键．
练习册系列答案
相关题目
利用下列图形验证勾股定理，如图中所有的四边形都是正方形，三角形都是直角三角形，如图（1）（2）．
如图，是某战役缴获敌人防御工事坐标地图的碎片，依稀可见：一号暗堡A的坐标为（4，3），五号暗堡B的坐标为（-2，3）．另有情报得知敌军指挥部的坐标为（-3，-2）．请问你能找到敌军的指挥部吗？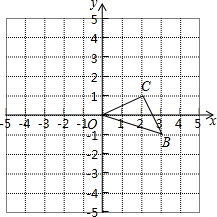
如图，已知O是坐标原点，B、C两点的坐标分别为（3，-1）、（2，1）．