题目内容
已知：如图，矩形ABCD的对角线相交于点O，DE∥AC，AE∥DB，AE、DE交于点E．求证：四边形DOAE是菱形．考点：菱形的判定,矩形的性质
专题：证明题
分析：首先根据两组对边分别平行的四边形是平行四边形可由条件DE∥AC，AE∥DB得四边形AODE是平行四边形，然后根据矩形的性质：矩形的对角线相等且互相平分，可得AO=DO，再根据组邻边相等的平行四边形是菱形证出四边形DOAE是菱形．
解答：证明：∵DE∥AC，AE∥DB，
∴四边形AODE是平行四边形，
∵矩形ABCD的对角线相交于点O，
∴AO=DO，
∴四边形DOAE是菱形．
∴四边形AODE是平行四边形，
∵矩形ABCD的对角线相交于点O，
∴AO=DO，
∴四边形DOAE是菱形．
点评：此题主要考查了菱形的判定，以及矩形的性质，关键是掌握菱形的判定定理：①菱形定义：一组邻边相等的平行四边形是菱形；②四条边都相等的四边形是菱形．③对角线互相垂直的平行四边形是菱形．
练习册系列答案
名题金卷系列答案
相关题目
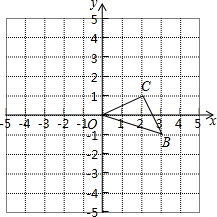如图，已知O是坐标原点，B、C两点的坐标分别为（3，-1）、（2，1）．
完成下列推理过程．已知：如图AD⊥BC，EF⊥BC，∠1=∠2，求证：DG∥AB．
如图，AB∥CD，∠1=50°，∠2=110°，求∠3的度数．