题目内容
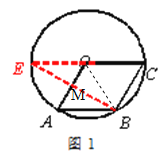
【题目】如图,A,B,C是⊙O上的三上点,且四边形OABC是菱形,请用无刻度直尺完成下列作图。
(1)如图①,作出线段OA的垂直平分线;
(2)如图②,作出线段BC的垂直平分线。


图① 图②
【答案】见解析
【解析】(1)延长CO交⊙O于点E,连接BE交OA于M.由OABC是菱形的性质得到OC∥AB,OC=AB,通过证明△EOM≌BAM,得到AM=OM.连接OB,得到△OAB是等边三角形,即可得到结论;
(2)在图(1)的基础上,连接AC,交OB于N,作直线MN交BC于F,作直线OF.
由OABC是菱形,得到ON=BN,从而得到MN∥AB,由平行线等分线段定理得到CF=BF,再由等腰三角形的性质即可得出结论.
(1)延长CO交⊙O于点E,连接BE交OA于M.
∵OABC是菱形,∴OC∥AB,OC=AB.
∵EO=OC,∴EO=AB.
∵OC∥AB,∴∠E=∠MBA,∠EOM=∠BAM,∴△EOM≌BAM,∴AM=OM.连接OB,则OB=OA=AB,∴△OAB是等边三角形,∴BM⊥OA,∴BE是OA的垂直平分线.
(2)在图(1)的基础上,连接AC,交OB于N,作直线MN交BC于F,作直线OF.
∵OABC是菱形,∴ON=BN.
∵OM=AM,∴MN∥AB,∴CF=BF.
∵OC=OB,∴OF⊥BC,∴OF为BC的垂直平分线.


【题目】2019年4月23日是第24个世界读书日.为了推进中华传统文化教育,营造浓郁的读书氛围,某校举办了“让读书成为习惯,让书香飘满校园”主题活动,为此特为七年级两个班级订购了一批新的图书.七年级两个班级订购图书的情况如下表:

四大名著/套 | 老舍文集/套 | 总费用/元 | |
七年级(1)班 | 2 | 4 | 460 |
七年级(2)班 | 3 | 2 | 530 |
(1)求四大名著和老舍文集每套各是多少元?
(2)学校准备再购买四大名著和老舍文集共10套,总费用不超过800元,求学校最多能买几套四大名著?
【题目】某奶粉每袋的标准质量为![]() 克,在质量检测中,超过标准质量
克,在质量检测中,超过标准质量![]() 克记作
克记作![]() 克,若低于标准质量
克,若低于标准质量![]() 克以上(不包括
克以上(不包括![]() 克)的,则这袋奶粉不合格,现在抽取
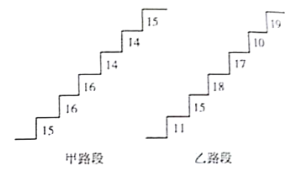
克)的,则这袋奶粉不合格,现在抽取![]() 袋样品进行质量检测,结果如下(单位:克):
袋样品进行质量检测,结果如下(单位:克):
袋号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
记作(克) |
|
|
|
|
|
|
|
|
|
|
(1)这![]() 袋奶粉中有哪几袋不合格?
袋奶粉中有哪几袋不合格?
(2)质量最少的是哪袋?它的实际质量是多少?
(3)这![]() 袋奶粉的平均质量是多少?
袋奶粉的平均质量是多少?