题目内容
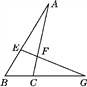
【题目】如图所示,BP是△ABC中∠ABC的平分线,CP是△ABC的外角∠ACM的平分线,如果∠ABP=20°,∠ACP=50°,那么∠A+∠P的度数为( )

A. 60° B. 70° C. 80° D. 90°
【答案】D
【解析】
根据角平分线性质得∠ABC=40°,∠ACM=100°,利用三角形外角性质即可求解.
解:∵BP是△ABC中∠ABC的平分线,CP是△ABC的外角∠ACM的平分线,∠ABP=20°,∠ACP=50°,
∴∠ABC=2∠ABP=40°,∠ACM=2∠ACP=100°,
∴∠A=∠ACM-∠ABC=100°-40°=60°, ∠ACB=180°-∠ACM=80°
∴∠BCP=∠ACB+∠ACP=130°
∵∠PBC=20°
∴∠P=180°-∠PBC-∠BCP=30°,
∴∠A+∠P=90°.
故答案为:90°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某地区为了进一步缓解交通拥堵问题,决定修建一条长为6千米的公路.如果平均每天的修建费y(万元)与修建天数x(天)之间在30≤x≤120,具有一次函数的关系,如下表所示.
X | 50 | 60 | 90 | 120 |
y | 40 | 38 | 32 | 26 |
(1)求y关于x的函数解析式;
(2)后来在修建的过程中计划发生改变,政府决定多修2千米,因此在没有增减建设力量的情况下,修完这条路比计划晚了15天,求原计划每天的修建费.