Question

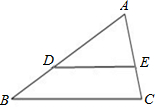（1）已知△ABC中，D、E分别是边AB、AC上的点，∠A=80°，∠C=70°，∠ADE=30°．求证：DE∥BC．
（2）阅读并补全下列命题的证明过程：
求证：在同一平面内，如果两条直线都和第三条直线垂直，那么这两条直线互相平行．
已知：如图，直线AB、CD、EF在同一平面内，AB⊥EF于点M，CD⊥EF于点N．
求证：______．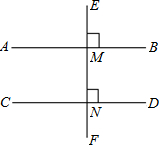
证明：∵AB⊥EF（已知），
∴∠AME=90°（垂直的定义）．
∵CD⊥EF（已知），
∴∠CNE=90°（垂直的定义）．
∵∠______=∠______．
∴______∥______．

Answer 1

（1）证明：∵∠A=80°，∠C=70°，
∴∠B=180°-∠A-∠C=180°-80°-70°=30°，
∵∠ADE=30°，
∴∠ADE=∠B=30°，
∴DE∥BC（同位角相等，两直线平行）；

（2）求证：AB∥CD，
证明：∵AB⊥EF（已知），
∴∠AME=90°（垂直的定义）．
∵CD⊥EF（已知），
∴∠CNE=90°（垂直的定义）．
∵∠AME=∠CNE，
∴AB∥CD．
故答案为：AB∥CD，∠AME，∠CNE，AB，CD．
分析：（1）根据三角形的内角和定理求出∠B=30°，再根据同位角相等，两直线平行即可判定DE∥BC；
（2）结合图形，根据证明过程可得∠AME=∠CNE，又这两个角是同位角，然后根据同位角相等两直线平行进行解答．
点评：本题考查了平行线的判定，分析图形找出同位角相等是解本题的关键．