题目内容
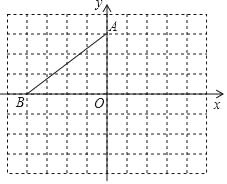
【题目】图①、图②、图③均为方形网格，每个小正方形的顶点称为格点，每个小正方形的边长均为1．
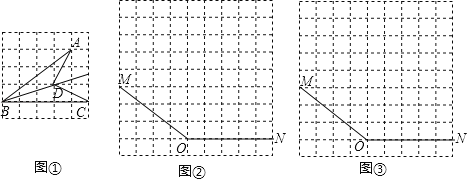
（探究）在图①中，点A、B、C、D均为格点．证明：BD平分∠ABC．
（应用）在图②、图③中，点M、O、N均为格点．
（1）利用（探究）的方法，在图②、图③中分别找到一个格点P，使OP平分∠MON．要求：图②、图③中所画的图形不相同，保留画图痕迹．
（2）cos∠MOP的值为 ．
【答案】【探究】：见解析；【应用】：（1）见解析；（2）
.
【解析】
探究：通过计算证明利用SSS证明三角形全等即可解决问题．
应用：（1）根据要求画出图形即可．图②中，构造边长为5的菱形即可解决问题．图③中，构造全等三角形解决问题即可．
（2）利用菱形的性质解决问题即可．
探究：证明：∵AB＝
＝5，BC＝5，
∴AB＝BC
∵AD＝CD＝
＝
．
BD＝BD，
∴△ABD≌△CBD（SSS），
∴∠ABD＝∠CBD，
即BD平分∠ABC．
应用：解：（1）射线OP如图所示．
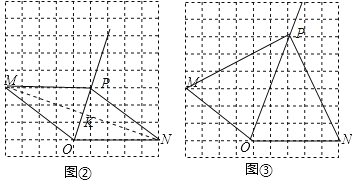
（2）如图②连接MN交OP于K，
∵四边形OMPN是菱形，
∴MN⊥OP，
∵OP＝
，OM＝5，
∴OK＝
，
∴cos∠MOP＝
＝．
练习册系列答案
相关题目
