题目内容
如图,等腰梯形ABCD中,AD∥BC,AB=5,BC=10,高AG=4,E为BC边上的一个动点(不与B、C重合).F是腰AB上的一点,且EF⊥AB、连接DE,DF.
(1)求证:△BEF∽△BAG;
(2)当点E在线段BC上运动时,设BE=x.△DEF的面积为y.①请你求出y和x之间的函数关系式,并写出自变量的取值范围;②求当x为何值时,y有最大(小)值.
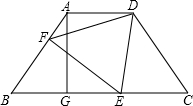
(1)求证:△BEF∽△BAG;
(2)当点E在线段BC上运动时,设BE=x.△DEF的面积为y.①请你求出y和x之间的函数关系式,并写出自变量的取值范围;②求当x为何值时,y有最大(小)值.

(1)∵AG⊥BC,EF⊥AB,
∴∠AGB=∠EFB=90°,∠B=∠B,
∴△BEF∽△BAG;
(2)∵△BEF∽△BAG,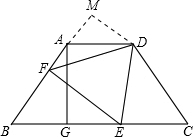
∴BF=
x,EF=
x,
作DM⊥AB于M,得△BEF∽△ADM,
∴
=
,
∴DM=
,
∴S△DAF=8-
x,
∵S梯形ABCD=28,S△DEC=20-2x,
∴y=S梯形ABCD-S△BEF-S△DEC-S△DAF=-
x2+
x,
∵当点F于点A重合时BF最长,此时
x=5,解得x=
,
∴0<x≤
,
∴当x=
,y有最大值.
∴∠AGB=∠EFB=90°,∠B=∠B,
∴△BEF∽△BAG;
(2)∵△BEF∽△BAG,

∴BF=
| 3 |
| 5 |
| 4 |
| 5 |
作DM⊥AB于M,得△BEF∽△ADM,
∴
| DM |
| 4 |
| 4 |
| 5 |
∴DM=
| 16 |
| 5 |
∴S△DAF=8-
| 24 |
| 25 |
∵S梯形ABCD=28,S△DEC=20-2x,
∴y=S梯形ABCD-S△BEF-S△DEC-S△DAF=-
| 6 |
| 25 |
| 74 |
| 25 |
∵当点F于点A重合时BF最长,此时
| 3 |
| 5 |
| 25 |
| 3 |
∴0<x≤
| 25 |
| 3 |
∴当x=
| 37 |
| 6 |

练习册系列答案
相关题目



