题目内容
(1)在图1中,平行四边形ABCD的顶点A,B,C,D的坐标(如图),请写出图中的顶点C的坐标( _________ , _________ ).
(2)在图2中,平行四边形ABCD的顶点A,B,C,D的坐标(如图),求出图中的标点C的坐标,并说明理由(C点坐标用含c,d,e的代数式表示).
归纳与发现
(3)通过对图1,2的观察,你会发现:图3中的平行四边形ABCD的顶点坐标为A(a,b),B(c,d),C(m,n),D(e,f)时,则横坐标a,c,m,e之间的等量关系为 _________ .
(1) C(5,2);(2) C(e+c,d);(3) a+m=c+e.
解析试题分析:(1)由四边形ABCD是平行四边形,点A(0,0),D(4,0),B(1,2),即可求得答案;
(2)首先过点B作BM⊥AD于M,过点C作CN⊥AD于N,易证得△AMB≌△DNC,然后由全等三角形的性质,求得答案;
(3)结合(2)可得a-c=e-m,继而求得答案.
试题解析:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=4,
∵B(1,2),
∴C(5,2);
(2)C(e+c,d);
证明如下:过点B作BM⊥AD于M,过点C作CN⊥AD于N,
在平行四边形ABCD中,AB=CD,AB∥CD,
∴∠BAM=∠CDN,
∵∠AMB=∠DNC=90°,
在△AMB和△CDN中, ,
,
∴△AMB≌△DNC(AAS),
∴AM=DN,BM=CN,
∴C点坐标为(e+c,d);
(3)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,BC∥AD,BC=AD,
∴a-c=e-m,
即a+m=c+e.
考点:1.平行四边形的性质;2.坐标与图形性质.

如图是丁丁画的一张脸的示意图,如果用(0,2)表示左眼,用(2,2)表示右眼,那么嘴的位置可以表示成( )
| A.(1,0) | B.(-1,0) | C.(-1,1) | D.(1,-1) |
对于函数y=-3x+1,下列结论正确的是( )
| A.它的图像必经过点(-1,3) |
| B.它的图象经过第一、二、三象限 |
C.当x> 时,y<0 时,y<0 |
| D.y的值随x值的增大而增大 |
如图,反比例函数 和正比例函数
和正比例函数 的图象交于
的图象交于 、
、 两点,则
两点,则 的解集是
的解集是
A.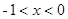 | B. 或 或 |
C. 或 或 | D.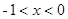 或 或 |
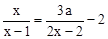 有非负数解,则a的取值范围是 .
有非负数解,则a的取值范围是 . 污水处理条件,决定购买A、B两种型号的污水处理设备
污水处理条件,决定购买A、B两种型号的污水处理设备



 轴的负方向平移6个单位,它与点 重合。
轴的负方向平移6个单位,它与点 重合。 轴是什么关系?
轴是什么关系? 在同一坐标系数中的大致图象是
在同一坐标系数中的大致图象是


