Question

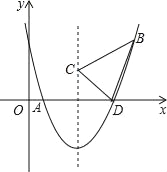
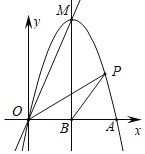
【题目】如图，抛物线y＝ax2+bx（a≠0）交x轴正半轴于点A，直线y＝2x经过抛物线的顶点M．已知该抛物线的对称轴为直线x＝2，交x轴于点B．

（1）求M点的坐标及a，b的值；

（2）P是第一象限内抛物线上的一点，且在对称轴的右侧，连接OP，BP．设点P的横坐标为m，△OBP的面积为S，当m为多少时，s＝．

Answer 1

【答案】（1）M（2，4），；（2）m的值为．

【解析】

（1）通过直线y=2x确定M点的坐标，然后利用对称轴方程和二次函数图象上点的坐标特征列关于a、b的方程组，再解方程组得到a、b的值；

（2）设P（m，-m2+4m），利用三角形面积公式得到×2×（-m2+4m）=，然后解方程求出即可得到满足条件的m的值．

解：（1）将x＝2代入y＝2x得y＝4

∴M（2，4），

根据题意得:

，

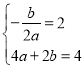解得；

（2）抛物线解析式为y＝﹣x2+4x，

设P（m，﹣m2+4m），B（2，0）

依题意得：×2×（﹣m2+4m）＝，

即：m2﹣4m＝﹣，

解得m1＝，m2＝，

∵P是第一象限内抛物线上的一点，且在对称轴的右侧，

∴m的值为．