题目内容
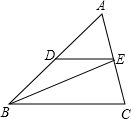 如图,已知:DE∥BC,BE是∠ABC的平分线,∠A=50°,∠C=70°,试求∠DEB、∠ADE、∠BEC的度数.
如图,已知:DE∥BC,BE是∠ABC的平分线,∠A=50°,∠C=70°,试求∠DEB、∠ADE、∠BEC的度数.
分析:首先由三角形的内角和定理,求得∠ADE的度数,又由BE是∠ABC的平分线,即可求得∠EBC的度数,然后由DE∥BC,根据两直线平行,同位角相等与两直线平行,内错角相等,求得∠DEB、∠ADE的度数,又由内角和定理,求得∠BEC的度数.
解答:解:∵∠A=50°,∠C=70°,
∴∠ABC=180°-∠A-∠C=180°-50°-70°=60°,
∵DE∥BC,
∴∠ADE=∠ABC=60°,
∵BE是∠ABC的平分线,
∴∠EBC=
∠ABC=30°,
∴∠DEB=∠EBC=30°,
∴∠BEC=180°-∠EBC-∠C=180°-30°-70°=80°.
∴∠DEB=30°,∠ADE=60°,∠BEC=80°.
∴∠ABC=180°-∠A-∠C=180°-50°-70°=60°,
∵DE∥BC,
∴∠ADE=∠ABC=60°,
∵BE是∠ABC的平分线,
∴∠EBC=
| 1 |
| 2 |
∴∠DEB=∠EBC=30°,
∴∠BEC=180°-∠EBC-∠C=180°-30°-70°=80°.
∴∠DEB=30°,∠ADE=60°,∠BEC=80°.
点评:此题考查了平行线的性质,角平分线的定义与内角和定理.此题难度不大,解题的关键是掌握两直线平行,同位角相等与两直线平行,内错角相等.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案
相关题目
 如图,已知AB∥DE,AB=DE,AF=DC,求证:四边形BCEF是平行四边形.
如图,已知AB∥DE,AB=DE,AF=DC,求证:四边形BCEF是平行四边形.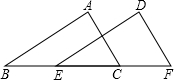 如图,已知AB=DE,AC=DF,要使△ABC≌△DEF,还需要补充一个条件,你补充的条件是:
如图,已知AB=DE,AC=DF,要使△ABC≌△DEF,还需要补充一个条件,你补充的条件是: 如图,已知:DE∥BC,AD:DB=1:2,DE=2,则BC=( )
如图,已知:DE∥BC,AD:DB=1:2,DE=2,则BC=( ) 如图,已知AB∥DE,BC∥EF,D,C在AF上,且AD=CF,请补充完整过程,说明△ABC≌△DEF的理由.
如图,已知AB∥DE,BC∥EF,D,C在AF上,且AD=CF,请补充完整过程,说明△ABC≌△DEF的理由.
 如图,已知AC∥DE,∠1=∠2.求证:AB∥CD.
如图,已知AC∥DE,∠1=∠2.求证:AB∥CD.