题目内容
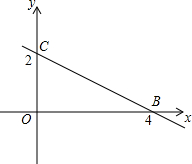
二次函数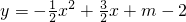 的图象与x轴交于A、两点(点A在点B左边),与y轴交于C点,且∠ACB=90°.
的图象与x轴交于A、两点(点A在点B左边),与y轴交于C点,且∠ACB=90°.
(1)求这个二次函数的解析式;
(2)设计两种方案:作一条与y轴不重合,与△A BC两边相交的直线,使截得的三角形与△ABC相似,并且面积为△BOC面积的 ,写出所截得的三角形三个顶点的坐标(注:设计的方案不必证明).
,写出所截得的三角形三个顶点的坐标(注:设计的方案不必证明).
解:(1)设A(x1,0),B(X2,0),则x1x2=-2(m-2),OA=-X1,OB=x2,
又C(0,m-2),则OC=m-2,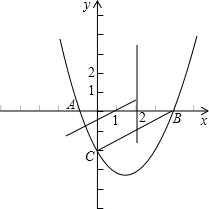
由△AOC∽△COB,得OC2=OA•OB=-x1x2,
即(m-2)2=2(m-2),又m-2>0,
∴m=4,得y=-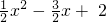 ;
;
(2)方案一:分别取OB,BC的中点O1,C1,连接O1C1,
可得△BO1C1三个顶点的坐标,B(4,0),O1(2,0),C1(2,1)
方案二:在AB上取AB2=AC= ,在AC上取AO2=AO=1,作直线O2B2,
,在AC上取AO2=AO=1,作直线O2B2,
可得△B2O2A三个顶点的坐标,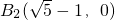 ,
,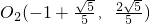 ,A(-1,0).
,A(-1,0).
分析:(1)A、B、C三点坐标可用m的代数式表示,利用相似三角形性质建立含m的方程;
(2)通过特殊点,构造相似三角形基本图形,确定设计方案.
点评:此题主要考查了解函数与几何结合的综合题,善于求点的坐标,进而求出函数解析式是解题的基础;而充分发挥形的因素,数形互助,把证明与计算相结合是解题的关键.
又C(0,m-2),则OC=m-2,
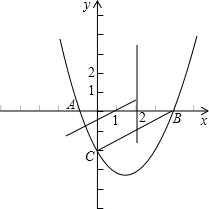
由△AOC∽△COB,得OC2=OA•OB=-x1x2,
即(m-2)2=2(m-2),又m-2>0,
∴m=4,得y=-
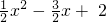 ;
;(2)方案一:分别取OB,BC的中点O1,C1,连接O1C1,
可得△BO1C1三个顶点的坐标,B(4,0),O1(2,0),C1(2,1)
方案二:在AB上取AB2=AC=
 ,在AC上取AO2=AO=1,作直线O2B2,
,在AC上取AO2=AO=1,作直线O2B2,可得△B2O2A三个顶点的坐标,
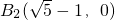 ,
,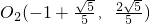 ,A(-1,0).
,A(-1,0).分析:(1)A、B、C三点坐标可用m的代数式表示,利用相似三角形性质建立含m的方程;
(2)通过特殊点,构造相似三角形基本图形,确定设计方案.
点评:此题主要考查了解函数与几何结合的综合题,善于求点的坐标,进而求出函数解析式是解题的基础;而充分发挥形的因素,数形互助,把证明与计算相结合是解题的关键.

练习册系列答案
相关题目
 为y=ax2-3ax-4a(a<0).
为y=ax2-3ax-4a(a<0).