题目内容
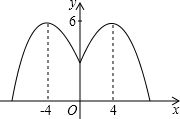
某游乐园要建一个直径为20m的圆形喷水池,计划在喷水池的中心安装一个大的喷水头,使喷出的水柱中心4m处达到最高,高度为6m,那么这个喷水头应设计的高度为______m.
∵喷出的水柱中心4m处达到最高,高度为6m,
∴抛物线的顶点坐标为(4,6)或(-4,6),
∵圆形喷水池的直径为20m,
∴抛物线与x轴的交点坐标为(10,0)或(-10,0),
设抛物线解析式为y=a1(x-4)2+6或y=a2(x+4)2+6,
由x=10,y=0得,36a1+6=0,解得a1=-
,
由x=-10,y=0得,36a1+6=0,解得a1=-
,
所以,函数解析式为y=-
(x-4)2+6或y=-
(x+4)2+6,
当x=0时,y=-
×16+6=
,
即这个喷水头应设计的高度为
m.
故答案为:
.
∴抛物线的顶点坐标为(4,6)或(-4,6),
∵圆形喷水池的直径为20m,
∴抛物线与x轴的交点坐标为(10,0)或(-10,0),
设抛物线解析式为y=a1(x-4)2+6或y=a2(x+4)2+6,
由x=10,y=0得,36a1+6=0,解得a1=-
| 1 |
| 6 |
由x=-10,y=0得,36a1+6=0,解得a1=-
| 1 |
| 6 |
所以,函数解析式为y=-
| 1 |
| 6 |
| 1 |
| 6 |
当x=0时,y=-
| 1 |
| 6 |
| 10 |
| 3 |
即这个喷水头应设计的高度为
| 10 |
| 3 |
故答案为:
| 10 |
| 3 |


练习册系列答案
相关题目
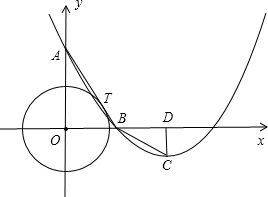 A(0,4)作⊙O的切线交x轴于点B,T是切点,抛物线y=ax2+bx+c的顶点为C(3,-
A(0,4)作⊙O的切线交x轴于点B,T是切点,抛物线y=ax2+bx+c的顶点为C(3,-
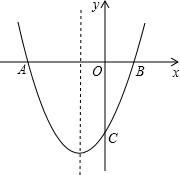


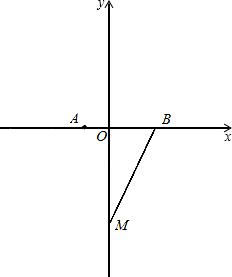 点M在y轴的负半轴上,且|AB|=6,cos∠OBM=
点M在y轴的负半轴上,且|AB|=6,cos∠OBM=