题目内容
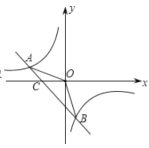
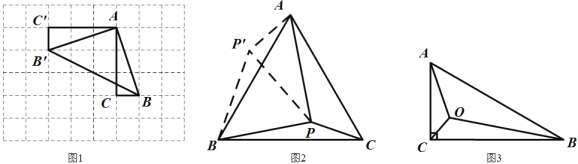
【题目】(1)如图 1,在边长为 1 个单位长度的小正方形组成的网格中,ABC 的三个顶点均在格点上.现将ABC 绕点 A 按顺时针方向旋转 90°,点 B 的对应点为B′,点 C 的对应点为C′, 连接 BB′,如图所示则∠AB′B= .
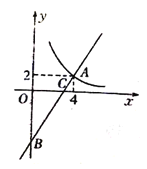
(2)如图 2,在等边ABC 内有一点 P,且 PA=2,PB=![]() ,PC=1,如果将△BPC 绕点 B 逆时针旋转 60°得出△ABP′,求∠BPC 的度数和 PP′的长;
,PC=1,如果将△BPC 绕点 B 逆时针旋转 60°得出△ABP′,求∠BPC 的度数和 PP′的长;
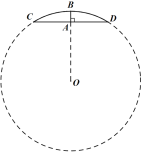
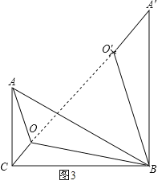
(3)如图3,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点O为
,点O为![]() 内一点,连接AO,BO,CO,且
内一点,连接AO,BO,CO,且![]() ,求
,求![]() 的值.
的值.
【答案】(1)45°;(2)∠BPC=150°,PP′=![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据旋转的性质,得到△ABB’是等腰直角三角形,即可得到答案;
(2)根据旋转的性质,BP=BP’,∠PBP’=60°,则![]() 是等边三角形,则
是等边三角形,则![]() ,
,![]() ,由
,由![]() 利用勾股定理的逆定理,得到
利用勾股定理的逆定理,得到![]() 是直角三角形,则
是直角三角形,则![]() ,即可得到∠BPC;
,即可得到∠BPC;
(3)将△![]() 绕点B顺时针旋转
绕点B顺时针旋转![]() 至△
至△![]() 处,连接
处,连接![]() ,利用直角三角形的性质求出AB,BC,然后利用旋转的性质,得到
,利用直角三角形的性质求出AB,BC,然后利用旋转的性质,得到![]() 是等边三角形,然后得到
是等边三角形,然后得到![]() 四点共线,然后利用勾股定理求出
四点共线,然后利用勾股定理求出![]() 的长度,即可得到
的长度,即可得到![]() .
.
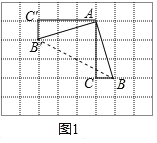
解:如图1所示,连接BB',将△ABC绕点A按顺时针方向旋转90°,
∴AB=AB',∠B'AB=90°,
∴∠AB'B=45°.
故答案为:45°;
(2)∵△ABC是等边三角形,
∴∠ABC=60°,
将△BPC绕点B顺时针旋转60°得出△ABP',如图2,
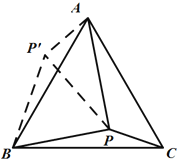
∴AP'=CP=1,BP'=BP=![]() ,∠PBC=∠P'BA,∠AP'B=∠BPC.
,∠PBC=∠P'BA,∠AP'B=∠BPC.
∵∠PBC+∠ABP=∠ABC=60°,
∴∠ABP'+∠ABP=∠ABC=60°,
∴△BPP'是等边三角形,
∴PP'=![]() ,∠BP'P=60°.
,∠BP'P=60°.
∵AP'=1,AP=2,
∴![]() ,
,
∴![]() ,
,
∴∠AP'P=90°,则△PP'A是直角三角形,
∴![]() ;
;
(3)如图3,将△![]() 绕点B顺时针旋转
绕点B顺时针旋转![]() 至△
至△![]() 处,连接
处,连接![]() ,
,
![]() 在
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 绕点B顺时针方向旋转
绕点B顺时针方向旋转![]() ,
,
![]() 如图所示;
如图所示;
![]() ,
,
![]() 绕点B顺时针方向旋转
绕点B顺时针方向旋转![]() ,得到
,得到![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 、O、
、O、![]() 、
、![]() 四点共线,
四点共线,
在![]() 中,
中,![]() ,
,
![]() .
.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案