题目内容
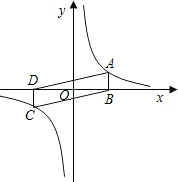 如图,A,C是函数y=
如图,A,C是函数y=| k |
| x |
A、
| ||
| B、2k | ||
| C、4k | ||
| D、k |
分析:由于A、C在反比例函数图象上且关于原点对称,根据反比例函数y=
中k的几何意义,S△ABD=S△CDB,则四边形ABCD的面积S即可求出.
| k |
| x |
解答:解:∵A,C是函数y=
(k≠0)的图象上关于原点对称的任意两点,
∴若假设A点坐标为(x,y),
则C点坐标为(-x,-y).
∴BD=2x,AB=CD=y,
∴S四边形ABCD=S△ABD+S△CBD=
BD•AB+
BD•CD=2xy=2k.
故四边形ABCD的面积S是2k.
故选B.
| k |
| x |
∴若假设A点坐标为(x,y),
则C点坐标为(-x,-y).
∴BD=2x,AB=CD=y,
∴S四边形ABCD=S△ABD+S△CBD=
| 1 |
| 2 |
| 1 |
| 2 |
故四边形ABCD的面积S是2k.
故选B.
点评:本题主要考查反比例函数中比例系数k的几何意义和函数图象的对称性,难易程度适中,是中考较常见的考查点.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
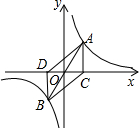 如图,A,B是函数
如图,A,B是函数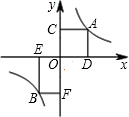 如图,A、B是函数
如图,A、B是函数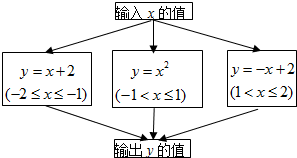 如图所示的程序是函数型的数值转换程序,其中-2≤x≤2.
如图所示的程序是函数型的数值转换程序,其中-2≤x≤2. 如图,A、B是函数
如图,A、B是函数 如图,A,C是函数
如图,A,C是函数