题目内容
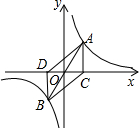 如图,A,B是函数y=
如图,A,B是函数y=| 1 | x |
分析:根据题意,得到四边形ADBC是平行四边形,则平行四边形的面积即为三角形AOC的面积的4倍.根据点A是反比例函数图象上一点,则三角形AOC的面积即为
=
,从而求得四边形的面积.
| |k| |
| 2 |
| 1 |
| 2 |
解答:解:∵A,B是函数y=
的图象上关于原点O对称的任意两点,
∴OA=OB,OC=OD,xy=1,
∴四边形ADBC是平行四边形,三角形AOC的面积是
.
∴平行四边形的面积=三角形AOC的面积的4倍=2.
故答案为2.
| 1 |
| x |
∴OA=OB,OC=OD,xy=1,
∴四边形ADBC是平行四边形,三角形AOC的面积是
| 1 |
| 2 |
∴平行四边形的面积=三角形AOC的面积的4倍=2.
故答案为2.
点评:此题考查了中心对称的性质、平行四边形的判定及性质以及反比例函数的性质.注意:从反比例函数图象上任意一点向x轴或y轴引垂线,则这点、原点、垂足所组成的三角形的面积是
.
| |k| |
| 2 |

练习册系列答案
相关题目
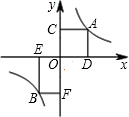 如图,A、B是函数
如图,A、B是函数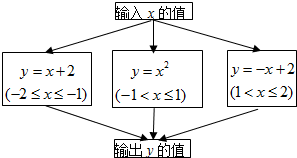 如图所示的程序是函数型的数值转换程序,其中-2≤x≤2.
如图所示的程序是函数型的数值转换程序,其中-2≤x≤2. 如图,A、B是函数
如图,A、B是函数 如图,A,C是函数
如图,A,C是函数