题目内容
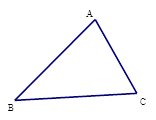
已知:如图,∠ABC,∠ACB的平分线相交于点F,过F作DE∥BC,交AB于D,交AC于E.试探索BD,CE与DE之间的数量关系,并证明你的结论.

DE=BD+CE.理由见解析
DE=BD+CE.理由:
∵BF平分∠ABC,
∴∠ABF=∠FBC.
∴DE∥BC,
∴∠DFB=∠FBC.
∴∠ABF=∠DFB.
∴DB=DF.
同理EF=EC.
∴DB+EC=DF+FE=DE.
根据角平分线的定义以及平行线的性质可证得:BD=DF,EF=EC,结合图形即可得出结论.
∵BF平分∠ABC,
∴∠ABF=∠FBC.
∴DE∥BC,
∴∠DFB=∠FBC.
∴∠ABF=∠DFB.
∴DB=DF.
同理EF=EC.
∴DB+EC=DF+FE=DE.
根据角平分线的定义以及平行线的性质可证得:BD=DF,EF=EC,结合图形即可得出结论.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
 ,
, ,
, .问
.问 吗?为什么?
吗?为什么?


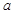 ∥
∥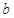 .直线
.直线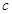 与直线
与直线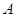 、点
、点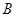 ,
, ,垂足为点
,垂足为点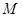 ,若
,若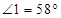 ,则
,则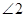 = _________。
= _________。