题目内容
【题目】如图,在△ABC中,AB=AC,∠A=36°,BE平分∠ABC,CD平分∠ACB,CD交BE 于点F,那么图中的等腰三角形共有( )个.
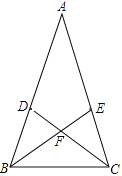
A. 6B. 7C. 8D. 9
【答案】C
【解析】
由已知可得∠ABC=∠ACB=72°,继而根据角平分线的定义可得∠ABE=∠ACD=∠EBC=∠DCB=36°,再根据三角形外角的性质可得∠BDC=∠BEC=72°,根据三角形内角定理可得∠CFE=∠BFD=72°,然后根据有两个角相等的三角形是等腰三角形进行判断即可得答案.
∵AB=AC,∠A=36°,
∴∠ABC=∠ACB=72°;
∵CD、BE分别平分∠ABC、∠ACB,
∴∠ABE=∠ACD=∠EBC=∠DCB=36°,
∴△ABE、△ACD、△BFC为等腰三角形,
∵∠BDC=∠A+∠ACD,∠BEC=∠A+∠ABE,
∴∠BDC=∠BEC=72°,
∴∠CFE=∠BFD=180°-∠ABE-∠BDC=180°-36°-72°=72°,
∴∠BDF=∠BFD,∠CFE=∠CEF,∠DBC=∠BDC,∠BCE=∠BEC,
∴△BDF、△CEF、△BDC,△BEC为等腰三角形,
又△ABC为等腰三角形,
∴图中的等腰三角形共有8个,
故选C.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
【题目】有这样一对数,如下表,第![]() 个数比第n个数大2(其中n是正整数)
个数比第n个数大2(其中n是正整数)
第1个 | 第2个 | 第3个 | 第4个 | 第5个 | …… |
a | b | c |
(1)第5个数表示为______;第7个数表示为_______.
(2)若第10个数是5,第11个数是8,第12个数为9,则a=______,b=_____,c=______.
(3)第2019个数可表示为________.