题目内容
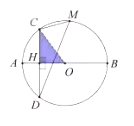
【题目】如图,线段 ![]() 是
是 ![]() 的直径,弦
的直径,弦 ![]() 于点
于点 ![]() ,点
,点 ![]() 是弧
是弧 ![]() 上任意一点,
上任意一点, ![]() .
.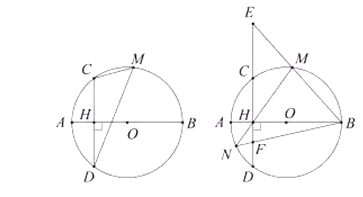
(1)求 ![]() 的半径
的半径 ![]() 的长度;
的长度;
(2)求 ![]() ;
;
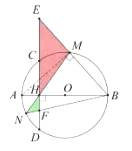
(3)直线 ![]() 交直线
交直线 ![]() 于点
于点 ![]() ,直线
,直线 ![]() 交
交 ![]() 于点
于点 ![]() ,连接
,连接 ![]() 交
交 ![]() 于点
于点 ![]() ,求
,求 ![]() 的值.
的值.
【答案】
(1)
解:连接OC,在Rt△COH中,
∵CH=4,OH=r-2,OC=r.
∴ (r-2)2+42=r2.
∴ r=5
(2)
解:∵弦CD与直径AB垂直,
∴ 弧AD=弧AC=![]() 弧CD.
弧CD.
∴ ∠AOC=![]() ∠COD.
∠COD.
∴∠CMD=![]() ∠COD.
∠COD.
∴ ∠CMD=∠AOC.
∴sin∠CMD=sin∠AOC.
在Rt△COH中,
∴sin∠AOC=![]() =
=![]() .
.
∴sin∠CMD=![]() .
.
(3)
解:连接AM,
∴∠AMB=90°.
在Rt△AMB中,
∴∠MAB+∠ABM=90°.
在Rt△EHB中,
∴∠E+∠ABM=90°.
∴∠MAB=∠E.
∵弧BM=弧BM,
∴∠MNB=∠MAB=∠E.
∵∠EHM=∠NHF.
∴△EHM∽△NHF
∴![]() =
=![]() .
.
∴HE.HF=HM.HN.
∵AB与MN交于点H,
∴HM.HN=HA.HB=HA.(2r-HA)=2×(10-2)=16.
∴HE.HF=16.
【解析】(1)连接OC,在Rt△COH中,根据勾股定理即可r.
(2)根据垂径定理即可得出弧AD=弧AC=![]() 弧CD;再根据同弧所对的圆周角等于圆心角的一半;得出 ∠CMD=∠AOC;在Rt△COH中,根据锐角三角函数定义即可得出答案.
弧CD;再根据同弧所对的圆周角等于圆心角的一半;得出 ∠CMD=∠AOC;在Rt△COH中,根据锐角三角函数定义即可得出答案.
(3)连接AM,则∠AMB=90°.在Rt△AMB中和Rt△EHB中,根据同角的余角相等即可∠MAB=∠E;再由三角形相似的判定和性质即可得HE.HF=HM.HN.
又由AB与MN交于点H,得出HM.HN=HA.HB=HA.(2r-HA)=2×(10-2)=16;从而求出HE.HF=16.
【考点精析】关于本题考查的余角和补角的特征和勾股定理的概念,需要了解互余、互补是指两个角的数量关系,与两个角的位置无关;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案.

 阅读快车系列答案
阅读快车系列答案