题目内容
【题目】对于平面直角坐标系xOy中的两个图形M和N,给出如下定义:若在图形M上存在一点A,图形N上存在两点B,C,使得△ABC是以BC为斜边且BC=2的等腰直角三角形,则称图形M与图形N具有关系φ(M,N).
(1)若图形X为一个点,图形Y为直线y=x,图形X与图形Y具有关系φ(X,Y),则点![]() ,P2(1,1),P3(2,﹣2)中可以是图形X的是 ;
,P2(1,1),P3(2,﹣2)中可以是图形X的是 ;
(2)已知点P(2,0),点Q(0,2),记线段PQ为图形X.
①当图形Y为直线y=x时,判断图形X与图形Y是否既具有关系φ(X,Y)又具有关系φ(Y,X),如果是,请分别求出图形X与图形Y中所有点A的坐标;如果不是,请说明理由;
②当图形Y为以T(t,0)为圆心,![]() 为半径的⊙T时,若图形X与图形Y具有关系φ(X,Y),求t的取值范围.
为半径的⊙T时,若图形X与图形Y具有关系φ(X,Y),求t的取值范围.
【答案】(1)![]() ;(2)①是;②
;(2)①是;②![]() 或
或![]() .
.
【解析】
(1)逐个点进行验证判断是否符合新定义的要求,要紧扣“使得△ABC是以BC为斜边且BC=2的等腰直角三角形”;
(2)①按照新定义和条件正确画出图形,结合图形进行求解;②分别找出t的最大值和最小值.
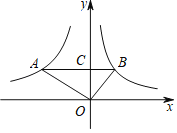
解:(1)P1;如图1,过P1作P1I⊥y轴交直线y=x于点C1,作P1B1⊥x轴于B1(B1与O重合),
∵P1(0,![]() ),
),
∴P1O=![]() ,
,
将y=![]() 代入y=x中,得x=
代入y=x中,得x=![]()
∴C1(![]() ,
,![]() ),即:C1P1=B1P1=
),即:C1P1=B1P1=![]()
∴![]() =
=![]() =2
=2
∴P1(0,![]() )与图形Y(直线y=x)具有关系φ(X,Y);
)与图形Y(直线y=x)具有关系φ(X,Y);
∵P2(1,1)在直线y=x上,
∴P2(1,1)与图形Y(直线y=x)不具有关系φ(X,Y);
∵P3(2,﹣2)
∴B3(﹣2,﹣2),C3(2,2),
∴B3C3=![]() =4
=4![]()
∴P3(2,﹣2)与图形Y(直线y=x)不具有关系φ(X,Y);
故答案为P1(0,![]() )
)
(2)①是,

如图2,在直线y=x上取点B,C,且BC=2,则满足△ABC是以BC为斜边的等腰直角三角形的点A,在到直线y=x距离为1的两条平行直线上.这两条平行直线与PQ分别交于A1,A2两点.故图形X与图形Y满足φ(X,Y).
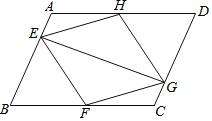
直线y=x与线段PQ交于点M(1,1),过点M作MH⊥y轴于H,与A1B交于点N,则MA1=1,![]() ,可得A1(
,可得A1(![]() ,
,![]() ).同理可求得A2(
).同理可求得A2(![]() ,
,![]() ).
).
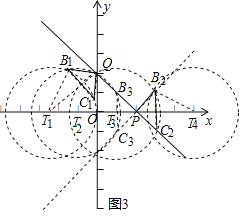
如图3,在线段PQ上取点B,C,且BC=2,则满足△ABC是以BC为斜边的等腰直角三角形的点A在图中的两条线段上,这两条线段与直线y=x交于A3,A4两点.故图形X与图形Y满足φ(Y,X).
同上可求得A3(![]() ,
,![]() ),A4(
),A4(![]() ,
,![]() ).
).
②如图3,当△QB1C1为等腰直角三角形,且斜边B1C1=2时,连接QT1交B1C1于S,
则QS=B1S=C1S=1,B1T1=![]() ,
,
∴T1S=2,T1Q=2+1=3
∴T1O=![]() =
=![]()
∴T1(﹣![]() ,0),
,0),
同理可求得:T2(﹣1,0),T3(2﹣![]() ,0),T4(5,0),
,0),T4(5,0),
∴![]() 或
或![]()